на нейтральной оси (там, где нормальное напряжение равно нулю) при z = 0 п притом в сечении, где Q(Jc) = Qmax.*

3 Qmax

(15.6)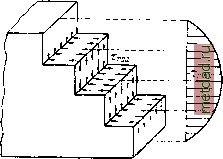

Фиг. 219.

Таким образом, наибольшее касательное напряжение при прямоугольном сечении будет в l раза больше среднего значения этого напряжения. На фиг. 219 изображена картина распределения касательных напряжений при положительной поперечной силе.

Наличие касательных напряжений в балке несколько искажает принятую нами раньше схему деформации балки. Мы считали, что под действием изгибающих моментов поперечные сечения, оставаясь плоскими, поворачиваются (фиг. 220, а). Под действием касательных напряжений элементы материала между двумя сечениями перекашиваются; этот перекос, в соответствии с изменением величины касательных напряжений, возрастает от краёв балки к нейтральной оси.

Поэтому сечения искривляются (фиг. 220, б). Однако это искривление почти не отражается на продольных деформациях волокон, что поз-

воляет пользоваться формулой с = -у и при наличии поперечной силы.

Поэтому кроме проверки прочности материала по наибольшим нормальным напряжениям (13.15)

<?тах= 11

производится проверка прочности материала и по наибольшим касательным напряжениям

maxmax fi

max =-- ] U О

Значения допускаемого напряжения [т] были даны выше.

Фиг. 220.

Для того чтобы получить представление о порядке величины т в балках прямоугольного сечения, рассмотрим числовой пример.

Найдём наибольшие нормальные и касательные напряжения для балки прямоугольного сечения при следующих данных: балка лежит на двух опорах и по всей длине /=4jr несёт равномерную нагрузку при =1,2 г/ж; Uax = 24 тм\ Qjnax = 2,4 т\ h = 27 СМ] =18 см; [7]= НО кг/см ; [х] = = 22 кгсм-.

240 ООО 6 18 . 27 3 . 2400

2 . 27 . 18

= 109,5 кгсм < 110 кг/см ;

= 7,5 кг/см < 22 кг/см.

Балка прямоугольного сечения, подобранная при нормальных напряжениях, равных допускаемым, имеет большое недонапряжение по касательным.

Однако на практике может встретиться и обратное явление; оно имеет место в случае, когда при большой поперечной силе изгибающий момент невелик. В этих случаях и при прямоугольном сечении величина касательных напряжений может оказаться решающей для определения размеров балки.

Формула касательных напряжений в балке прямбугольного сечения впервые была выведена русским инженером Д. И. Журавским при проектировании ) им деревянных мостов для железной дороги Петербург - Москва в 1855 г. Журавский воспользовался несколько иным и более трудным приёмом

для получения этой формулы, не применяя зависимости = Q, с которой

иногда совершенно напрасно связывают имя Шведлера.

§ 92. Касательные напряжения в балке двутаврового сечения.

Так как сечения двутавровых и тавровых балок можно рассматривать как составленные из прямоугольников, то с известным приближением можно распространить на них теорию, изложенную в

предыдущем параграфе. Таким образом, ка-р=\ сательные напряжения

Д в точке на расстоянии z

1-~\ от нейтральной оси для

-I двутаврового сечения ЩЩ (фиг. 221) выражаются

также формулой

95 (г)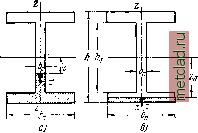

(15.3)

Фиг. 221.

Здесь .S (z) - по-прежнему статический момент относительно

нейтральной оси у части площади сечения между уровнем z и краем балки. Что касается величины b{z) - ширины сечения, то ей в дан-

Д. И. Ж у р а в с к и й, О мостах раскосной системы Гау, часть II, приложение III. Замечания относительно сопротивления бруска, подверженного силе, нормальной к его длине, стр. 130.

99998

(15.9)

В обоих случаях х меняется по параболической кривой.

Так как для двутаврового сечения толщина стенки обычно бывает незначительной, то в этом профиле касательные напряжения достигают довольно большой величины, и поэтому проверка их всегда является необходимой.

В месте перехода от полки (пояса) к стенке ширина меняется скачком; в знаменатель формулы (15.9) можем подставить значения и ftji и Ь. Для величины касательного напряжения мы на этом уровне получаем два значения. График распределения напряжений по оси стенки z - z получает вид, изображённый на фиг. 221, в и 222, а.

Надо помнить, что это результат подсчётов, сделанных в предположении, что формула (15.3) применима и к вычислению напряжений у места перехода от пояса к стенке. На самом деле резкое изменение ширины сечения вызывает местное перераспределение напряжений.

Более точные исследования показывают, что по линии, совпадающей с осью симметрии сечения, распределение касательных напряжений будет с достаточной точностью изображаться графиком фиг. 222, б\ по линии же 2-2, проходящей у самого края стенки, - кривой, показанной на фиг. 222, в; последний график показывает, что в точках у входящих углов сечения касательные напряжения теоретически достигают очень большой величины; на практике эти входящие углы скругляются, напряжения падают и их распределение в точках линии 2-2 примерно представляется кривой фиг. 222, г. Наибольшая ордината графиков фиг. 222, а, б и 2 примерно одинакова и относится к точкам на нейтральной оси.

ном случае приписан значок z\ это означает, что в знаменатель формулы (15.3) следует подставлять ширину сечения на уровне z. Как видно из вывода формулы (15.3), величина b входила множителем в слагаемое Ib dx, т. е. была поперечным размером площадки, по которой действовало напряжение таким образом, величина b была шириной балки на уровне z. Поэтому при применении формулы (15.3) к двутавровому сечению следует, вычисляя касательные напряжения на уровне z (фиг. 221, б), т. е. на площадках, попадающих в пределы полки, подставлять в знаменатель ширину пояса Ь, В этом случае формула (15.3) принимает вид:

- 877--hj

При вычислении же касательных напряжений на уровне z, т. е. на площадках, находящихся в пределах стенки, надо вместо Ь подставлять толщину стенки Ь. Формула тоже видоизменится: придётся брать статический момент двух прямоугольников (штриховка на фиг. 221, а). Если произвести вычисления, то получим: