§ 88. Приближённый метод вычисления моментов инерции площади.

В некоторых случаях очертание поперечного сечения оказывается настолько сложным, что его трудно разбить на простые элементы, особенно

если это очертание криволинейно. Тогда можно при\. ть следующий приближённый метод вычи -я момента инерции этой фигуры относые..но какой-нибудь оси у (фиг. 203).

Ра?теляем фигуру на полоски линиями, параллельными оси у\ ширину полосок t выбираем малой по сравнению с размерами фигуры. Тогда каждую из этих полосок можно принять за прямоугольник высотой t и переменной шириной Момент инерции каждой такой полоски относительно оси у будет равен: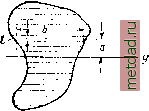

Фиг. 203.

Так как мы выбрали высоту полосок t малой, то слагаемым можно

пренебречь по сравнению с а tb. Тогда полный момент инерции фигуры будет равен:

JyI.a4b = Y,adF. (14.22)

Чтобы оценить точность этого метода, вычислим момент инерции относительно центральной оси прямоугольника, изображённого на фиг. 204;

прямоугольник взят потому, что ДЛЯ него легко подсчитать точное значение Jy, Так как мы вы-

20см

числяем момент инерции относительно оси симметрии, то достаточно вычислить момент инерции ДЛЯ верхней половины сечения и результат удвоить. Разделим верхнюю половину площади сечения на 5 ПОЛОСОК высотой по t = 2 см\ ширина всех полосок одинакова. Тогда

A = 2!Sfl2:=2. 10 . 2(12+ 32+ 5 + 72+ 92) = = 6600 см\

Точная величина этого момента инерции равна:

, № 10-20

У =--==-- = 6667 см\

Разница

Фиг. 204.

6667 - 6600 67

6667 ~6667/

Мы видим, что даже при таком грубом делении площади на полоски результат получается достаточно точным. В пределе мы и приходим к точному выражению для момента инерции.

При неправильном или криволинейном очертании фигуры кроме числового подсчёта по формуле (14.22) можно применить графический метод - построение верёвочного многоугольника. Начертим (фиг. 205) какую-либо фигуру в линейном масштабе л/1, проведём ось у и разделим рассматриваемую площадь на элементарные полоски bt. Приложим в центре тяжести каждой /г-й полоски условную (фиктивную) силу равную по числовой величине площади полоски; направление сил возьмём параллельно оси у.

Построим силовой многоугольник в масштабе 1 с произвольным полюсным расстоянием Я, проведём лучи и построим верёвочный многоугольник.

Возьмём в силовом многоугольнике какую-нибудь силу Fn\ продолжим стороны верёвочного многоугольника, пересекающиеся на линии этой силы в точке о, до пересечения их с осью у в точках k и т. Расстояние силы до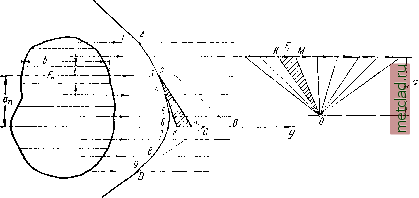

Фиг. 205.

оси у обозначим а. Заштрихованному на верёвочном многоугольнике треугольнику okm соответствует подобный ему треугольник ОКМ в силовом многоугольнике. Из подобия этих треугольников имеем:

km Fn

Произведение средних и крайних даёт нам

aFn = km

Умножим обе части этого равенства на л:

,z = /i -km- Н.

Произведение

an Ш= 2 . у а .

равно удвоенной площади заштрихованного треугольника okm.

Таким образом, момент инерции /г-й площадки (F = bt) относительно оси у численно равен площади заштрихованного треугольника okm, умноженной на удвоенное полюсное расстояние Н,

* Надо помнить, что Н входит в силовой многоугольник и, стало быть, выражается, как и силы в единицах площади. Если проделать эти вычисления для всех сил F и просуммировать полученные результаты, то момент инерции фигуры У, равный ТЕа, будет графически изображаться произведением полюсного расстояния М на удвоенную площадь ABCDA, ограниченную верёвочным многоугольником и продолжениями его крайних сторон. Называя величину этой площади имеем формулу:

Уз, = 2Ясо.

(I4j3)

>;, = :i=l,97 см2,0 см; = 1 = 8,00 см.

*) Здесь индексы при координатах площадок указывают: первый -ось (Уи а второй - номер площадки.

При вычислениях надо учитывать масштабы. Площадь <о измеряется на чертеже, изображённом в линейном масштабе п/1 (см/см\ а полюсное расстояние Н измеряется в масштабе сил ~ (см/см). Поэтому если мы на

чертеже измерили площадь ABCDA равной <о см, а полюсное расстояние М см, то

У = 2 о)/. 2.

Удобно выбирать высоту полосок одинаковой, тогда все будут пропорциональны ширинам полосок. Площадь <о может быть измерена планиметром. Нет нужды гнаться за большим числом полосок; мы видели выше, что достаточная точность получается при сравнительно широких полосках. Надо помнить, что описанный способ основан на пренебрежении собственными центральными моментами инерции полосок.

Применим теперь полученные в этой главе результаты к решению задач по проверке прочности балок с более сложным сечением.

§ 89. Пример расчёта балки несимметричного сечения.

Пример 57. Определить величину допускаемого изгибающего момента для балки, защемлённой одним концом в стену, если пара сил расположена на другом конце в главной плоскости инерции. Размеры сечения в мм показаны на фиг. 206. Пролёт балки / = = 0,6 м. Допускаемое напряжение [а] = 1600 кг/см.

Прежде всего необходимо найти положение центра тяжести сечения. Для этого выбираем произвольную систему координатных осей yiZi] удобно, чтобы вся фигура лежала в положительном квадранте. Расстояния центра тяжести сечения до этих осей найдутся по формулам:

Ус = у и с = у,

где Sy и Sg - статические моменты площади относительно осей ух и г,.

Для подсчёта статических моментов разобьём площадь нашей фигуры на 2 прямоугольника - вертикальный / и горизонтальный У/. Площадь фигуры равна F=\ 12-f-7 1 = 19,0 см. Статические моменты

5; = Fyi, 1 + F,j;i. 2 = 12 . 0,5 + 7 (1 + 3,5) = 37,5 см; 5; = /=,i +F2Zi.2 = 12. 6,0 + 7. 11,5=152,5 см\

Координаты центра тяжести:

37,5