Но условия перпендикулярности осей z и у а равенства нулю zydF могут быть выполнены и для несимметричного сечения

балки; для этого достаточно, чтобы ось <г, лежащая в плоскости действия сил, и нейтральная ось у были главными центральными осями инерции поперечного сечения балки. Тогда и условие перпендикулярности соблюдается, и интеграл J zydF, как центробежный момент инерции сечения относительно главных осей, снова будет равен нулю.

Значит, вместо условия совпадения плоскости внешних сил с плоскостью симметрии сечений балки можно ввести другое: чтобы плоскость действия внешних сил совпадала с одной из двух плоскостей, содержащих главные оси инерции поперечных сечений. Эти две плоскости в балке называются главными плоскостями инерции.

Тогда нейтральной осью будет вторая главная ось, перпендикулярная к плоскости внешних сил, и условие J zydF=0 будет ав-

томатически удовлетворено.

Так как при всякой форме поперечного сечения балки мы можем найти главные центральные оси инерции, то для балки любого поперечного сечения можно пользоваться выведенными формулами (13.9) и (13.13)

Mz maxM

с - -у и тах = -

при условии, что внешние силы лежат в одной из главных плоскостей инерции балки; J ]л W берутся относительно другой главной

§ 86. Распространение формулы для вычисления нормальных напряжений на случай несимметричного сечения балки.

Пользуясь равенством нулю центробежного момента инерции относительно главных осей, д:ожно показать, что формулы § 78 применимы при известных условиях и к несимметричным сечениям.

При выводе формулы для нормальных напряжений (§ 78) введённое нахми ограничение, что балка симметрична относительно плоскости действия внешних сил xz, понадобилось нам прежде всего для: 1) установления перпендикулярности нейтральной оси у к плоскости ZX, 2) доказательства того, что сумма моментов усилий dN относительно оси z равна нулю:

2]Ж, = 0, yJj;rfF=0, zydF = 0. (13.6)

(14.20)

где - момент инерции относительно оси v, а F-площадь фигуры. Если Jy и Jz - главные моменты инерции, то

lyyjy и

называются главными радиусами инерции.

Построим на главных осях инерции фигуры (оси у п эллипс с полуосями /у и отложив радиус iy перпендикулярно к оси у и радиус 1 перпендикулярно к оси z (фиг. 202). Этот эллипс называется центральным эллипсом инерции фигуры; уравнение его будет

где у и z - координаты точек эллипса.

Если iyz=zi=zi то эллипс инерции обращается в круг инерции с уравнением:

V См. главу XXX, Основы расчёта тонкостенных стержней на кручение и изгиб.

оси, перпендикулярной к плоскости действия внешних сил и являющейся нейтральной осью.

Как пример, можно указать балку зетового сечения (фиг. 201) с главными осями z и у. Приведённые выше формулы применимы к ней, если внешние силы будут лежать в плоскости Z или у; нейтральной осью в первом случае будет у, во втором Z, Так как нейтральные оси сечений и в этом случае перпендикулярны плоскости действия внешних сил, то ось балки при деформации будет оставаться в этой плоскости. Таким образом, расположение внешних сил в одной из главных плоскостей инерции балки и будет общим случаем плоского изгиба.

Фиг. 201. Надо заметить, что в некоторых случаях в балках

несимметричного (относительно оси, лежащей в плоскости действия сил) сечения появляется дополнительная система нормальных и касательных напряжений (§ 96), связанная с добавочным кручением балки *).

§ 87. Эллипс инерции.

Помимо аналитического, можно дать графическое изображение изменения моментов инерции при помощи построения так называемого эллипса инерции.

Введём новую величину - радиус инерции фигуры относительно ка-кой-либо оси. Радиусом инерции относительно оси v называется величина

§ 871

ЭЛЛИПС ИНЕРЦИИ

При помощи эллипса инерции можно графически найти радиус инерции ijc для любой оси X, составляющей с главной осью у угол fi (фиг. 202), а затем, следовательно, вычислить и момент инерции по формуле

(14.21)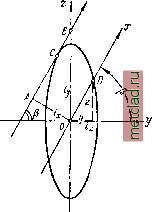

Для нахождения радиуса инерции надо провести к эллипсу касательную, параллельную оси х\ расстояние от центра эллипса до этой касательной (отрезок OA) и будет радиусом инерции /д.. Действительно, напишем выражение для Уд.:

У,.==У cosp + ysin*?.

Разделив обе части этой формулы на получим зависимость

/2 = i2cos*p + /sin2?.

Теперь напишем уравнение касательной к эллипсу инерции, составляющей с осью у угол р, и вычислим длину перпендикуляра OA, опущенного из центра эллипса на эту касательную. Уравнение эллипса в параметрической

у = ig cos ср; 2 = iy sin ср.

Координаты точки касания С отметим значком с:

yc=tz coscp; Zc = iy sin cp.

Уравнение касательной напишем в виде

z = ay-{-b.

Угловой её коэффициент равен:

= tg р;

с другой стороны, из уравнения эллипса

ординату b найдём, подставляя в уравнение касательной координаты точки С; после некоторых преобразований, получим:

Фи1\ 202.

форме имеет вид:

/ /jcos* p4-/§sin2p

sin cp

cosp

Квадрат длины перпендикуляра ОЛ, опущенного из центра О на касательную, равен:

Гу cos* Р + / sin* р

1+ *- cos*P(l+tg*P)

04*=.

что мы и хотели доказать.

Кроме указанного графического построения, изображающего зависимость между моментами инерции относительно различных осей, имеется ещё ряд графических приёмов, из которых рассмотрим лишь применение верёвочного многоугольника.