Проведём центральную ось Оу, момент инерции относительно этой оси назовём Jy. Проведём в плоскости фигуры ось у параллельно оси у на расстоянии а от неё. Найдём зависимость между Jy и Jy - моментом инерции относительно оси у. Для этого напишем выражения для Jy и Jy. Разобьём площадь фигуры на площадки dF\ расстояния каждой такой площадки до осей у и у назовём z и Zi. Тогда

JyzF и j;=z\dF. Но из чертежа имеем:

z = z-\-a,

следовательно:

j;= J + af dF= J (z -f 2a+ a) dF =

= zF-{-2a zdFa J

Первый из этих трёх интегралов - момент инерции относительно центральной оси Оу. Второй - статический момент относительно той же оси; он равен нулю, так как ось у проходит через центр тяжести фигуры. Наконец, третий интеграл равен площади фигуры F. Таким образом,

Jy = JyJaF, (14.7)

т. е. момент инерции относительно любой оси равен моменту инерции относительно центральной оси, проведённой параллельно t данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Значит, наша задача теперь свелась к вычислению только центральных моментов инерции; если мы их будем знать, то по формуле (14.7) сможем вычислить момент инерции относительно любой другой оси. Из формулы (14.7) следует, что центральный момент инерции является наименьшим среди моментов инерции относительно параллельных осей и для него мы получаем:

Найдём также центробежный момент инерции Jyg относительно осей yZi, параллельных центральным, если известен У, = j/z flfF

(фиг. 196). Так как по определению

Jyz= [yiZdF,

Фиг. 196.

где>1=> + , Zi=z-\-a, то

fyг=\{:y~b){zAra)dF =

= yzdF~{-ab dF + a у dF- Ь z dF.

F F F F

Так как два последних интеграла представляют собой статические моменты площади относительно центральных осей Оу и Oz, то они обращаются в нуль и, следовательно:

Jyz = Jyz + abF. (14.8)

Центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно этих центральных осей плюс произведение из площади фигуры на координаты её центра тяжести относительно новых осей.

§ 83. Зависимость между моментами инерции при повороте осейи

Центральных осей можно провести сколько угодно. Является вопрос, нельзя ли выразить мо.мент инерции относительно любой центральной оси в зависимости от момента инерции относительно одной или двух определённых осей. Для этого посмотрим, как будут меняться моменты инерции относительно двух взаимно перпендикулярных осей при повороте их на угол а.

Возьмём какую-либо фигуру и проведём через её центр тяжести О две взаимно перпендикулярные оси Оу и Oz (фиг. 197). Пусть нам известны осевые моменты инерции относительно этих осей Jy, J, а также центробежный момент инерции Jy. Начертим вторую систему координатных осей

Ух и 1, наклонённых к первым под углом а; положительное направление этого угла будем считать при повороте осей вокруг точки О против часовой стрелки. Начало координат О сохраняем. Выразим моменты относительно второй системы координатных осей Jy и J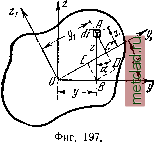

через известные моменты инерции

Напишем выражейия для моментов инерции осей:

относительно этих

i = 0£ +£C=0+iBD=3;cosa-{-zsina, \ i=AD - DC = AD - BE = 2C0sa-ysma. j

У1 = г

Подставляя эти значения у и в формулы (14.9), получим: Jj, = (г cos а -у sin а) dF -

== (z cos а -f-J/ sin a - 2yz sin a cos a) dF

y;=cos a Jг dF--sin a dF-sin 2a yzdF. (14.11) Аналогично:

= J (у cos a 2 sin a) dF

j; = sin a J dF+cos a J/dF+sin 2a JdF. (14.12)

Первые два интеграла выражений (14.11) и (14.12) представляют собой осевые моменты инерции и J, а последний - центробежный момент инерции площади относительно этих осей Jyg. Тогда:

j: = J cosa-4-J-Sina - sin 2а, ]

y; = y3,sin a--ycosa + J3,sin2a. j

Для решения задач могут понадобиться формулы перехода от одних осей к другим для центробежного момента инерции. При повороте осей (фиг. 197) имеем:

JyM = y\ZxdF,

где Ух и г, вычисляются по формулам (14.10); тогда

=sinacos oLzdF-sin а cos oLydF cosoLyzdF-s\na yzdF.

После преобразований получим:

j;, = 1 (iy sin 2a + Jy cos 2a. (14.14)

Из чертежа видно, что координаты площадки dF в системе fio-вёрнутых осей yxOzx будут: