Для треугольника (фиг. 190) момент инерции относительно оси АВ равен

в следующей главе будет показано, как вычислять момент инерции для сечения любой сложной формы относительно любой оси.

На практике из симметричных сечений встречаются чаще всего: для дерева - прямоугольник и круг, для металлов - двутавровое и тавровое сечения (фиг. 191). Для прокатных профилей можно пользоваться таблицами ОСТ (сортамент), в которых помещены размеры и

±

Фиг. 190.

Фиг. 191.

Фиг. 192.

величины J и W для профилей, выпускаемых заводами. Эти таблицы помещены в приложении IX и пользование ими показано на примере в следующем параграфе.

В балках, из металла обычно применяются сложные поперечные сечения, потому что в них материал может быть использован экономичнее, чем в таких сечениях, как прямоугольник и круг.

Мы видели (§ 58), что валы делают полыми, чтобы удалить ту часть материала, которая слабо работает. При изгибе балок материал около нейтральной оси принимает на себя малые нормальные напряжения [формула (13.9)] и также не может быть использован полностью. Поэтому целесообразнее переделать прямоугольное сечение так, чтобы удалить материал у нейтральной оси и часть его сэкономить, а часть перенести в верхнюю и нижнюю зоны балки, где он будет работать более интенсивно. Так получается (фиг. 192) из прямоугольного сечения профиль двутавра, обладающего той же прочностью и меньшим весом. Применение двутавра целесообразно при материалах, одинаково сопротивляющихся растяжению и сжатию (большинство металлов).

Сечения в виде тавра применяются или в случаях, вызываемых специальными конструктивными обстоятельствами, или для таких материалов, как чугун, бетон, у которых сопротивления растяжению

и сжатию резко разнятся между собой; последнее обстоятельство требует, чтобы напряжения в крайних волокнах были различными.

Как видно из изложенного, при решении вопроса о наиболее экономичном проектировании сечения следует стремиться к тому, чтобы при одной и той же площади F получить наибольший момент

сопротивления и момент инерции. Это ведёт к размещению большей части мате-тах риала подальше от нейтральной оси.

Однако для некоторых сечений можно увеличить момент сопротивления не добавлением, а, наоборот, путём срезки \ некоторой части сечения, наиболее уда-- Ш / ОМ лённой от нейтральной оси.

} Так, например, для круглого сече-

Фиг. 193. ния срезка заштрихованных сегментов

(фиг. 193) несколько увеличивает момент сопротивления, так как при этом мы уменьшаем момент инерции сечения в меньшей степени, чем расстояние до крайнего

волокна Zmax.

§ 81. Общий способ вычисления моментов инерции сложных сечений.

При проверке прочности частей конструкций нам приходится встречаться с сечениями довольно сложной формы, для которых нельзя вычислить момент инерции таким простым путём, каким мы пользовались для прямоугольника и круга в § 80.

Таким сечением может быть, например, тавр (фиг. 194, а), кольцевое сечение трубы, работающей на изгиб (авиационные кон-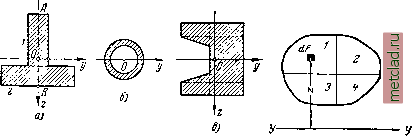

Фиг. 194.

Фиг. 195.

струкции) (фиг. 194, (5), кольцевое сечение шейки вала или ещё более сложное сечение (фиг. 194, в). Все эти сечения можно разбить на простейшие, как-то: прямоугольники, треугольники, круги и т. д. Можно показать, что момент инерции такой сложной фигуры является суммой моментов инерции частей, на которые мы её разбиваехМ.

§ 82] МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ 275

Возьмем (фиг. 195) какую угодно фигуру, изображающую поперечное сечение балки; в ее плоскости проведена ось у -у. Момент инерции этой фигуры относительно оси у-у равен (13.7);

где Z-расстояние элементарных площадок dF до оси у-у.

Разобьем взятую площадь на четыре части: Fi, F<y F и F, Теперь при вычислении момента инерции по формуле (13.7) можно сгруппировать слагаемые в подинтегральной функции так, чтобы отдельно произвести суммирование для каждой из выделенных четырех площадей, а затем эти суммы сложить. Величина интеграла от этого не изменится.

Наш интеграл разобьется на четыре интеграла, каждый из которых будет охватывать одну из площадей Fj, /2, F или F:

J = jzUF=zF J zFjzUF + z dF.

Каждый из этих интегралов представляет собой момент инерции соответствующей части площади относительно оси у-у; поэтому

= 4 + + (14.6)

где /у - момент инерции относительно оси у-у площади Fi, Jy - то же для площади и т. д.

Полученный результат можно формулировать так: момент инерции сложной фигуры равен сумме моментов инерции составных её частей. Поэтому, чтобы вычислить, например, момент инерции сечения, изображенного на фиг. 194, в, относительно оси Оу, необходимо найти моменты инерции прямоугольников и треугольников относительно оси Оу и затем сложить их. Таким образом, нам необходимо уметь вычислять момент инерции любой фигуры относительно любой оси, лежащей в её плоскости.

Решение этой задачи и составляет содержание настоящей главы.

§ 82. Зависимость между моментами инерции относительно параллельных осей, из которых одна - центральная.

Задачу - получить наиболее простые формулы для вычисления момента инерции любой фигуры относительно любой оси - мы решим в несколько приемов. Если взять серию осей, параллельных друг другу, то оказывается, что можно легко вычислить моменты инерции фигуры относительно любой из этих осей, зная ее момент инерции относительно оси, проходящей через центр тяжести фигуры параллельно выбранным осям.

Оси, проходящие через центр тяжести, мы будем называть центральными осями. Возьмем (фиг. 196) какую-нибудь фигуру.