Однако найти из полученного уравнения величину т мы пока не можем, так как ещё не знаем, как распределяются касательные напряжения по сечению.

В. Уравнения статики не дают возможности довести до конца решение задачи определения напряжений по сечению /-/. Задача оказывается статически неопределимой, и для окончания её решения нам придётся обратиться к рассмотрению деформаций стержня, показанных на фиг. 122 и 124.

Выделим (фиг. 124) на поверхности скручиваемого стержня до его деформации двумя смежными образующими аЬ и cd и двумя контурами смежных сечений 7-/ и 2-2 прямоугольник ABDC.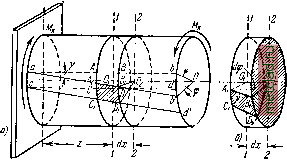

Фиг. 124.

После деформации оба сечения, J-7 и 2-2, повернутся относительно защемлённого конца на углы ср (сечение I-I) и 9:4 ? (сечение 2-2). На основании принятых гипотез оба сечения останутся плоскими, радиусы ОВ и 0И> OjC и OD останутся прямыми, а расстояние dx между сечениями /-/ и 2-2 останется без изменения. При таких условиях весь элемент ABDCOiO сместится и перекосится, так как его правая грань, совпадающая с сечением 2-2, повернётся на угол d относительно левой, совпадающей* с сечением 1-1, Прямоугольник ABDC займёт положение, показанное на фиг. 124 штриховкой. Перекошенный элемент AiBDiCfiiO показан на фиг. 125; там же пунктиром изображён вид этого элемента, если бы он не испытал перекоса, т. е. если бы его левая и правая грани обе повернулись на один и тот же угол.

Перекос, вызванный неодинаковым поворотом сечений 1-1 и 2-2, обращает прямые углы прямоугольника ABDC в тупые и острые; материал нашего элемента испытывает деформацию сдвига (фиг. 122 и 124). Величина этой деформации будет характеризоваться углом перекоса - относительным сдвигом; на поверхности стержня в прямоугольнике AiBDCi этот угол будет равен BAiBi, он обозначен на фиг. 125 буквой .

Как известно, деформация сдвига сопровождается возникновением касательных напряжений по граням перекашиваемого элемента (§ 54).

На фиг. 125 изображены эти напряжения, действующие на площадки, выделенные на правой грани (поперечное сечение 2-2) и горизонтальной поверхности элемента АВйСхОхО. Величину этих напряжений мы можем выразить через относительный сдвиг f, характеризующий перекос прямоугольника AiBiDiCx, по формуле (10.21): t = 7G.

Так как абсолютный сдвиг элемента на поверхности вала равен ВВ = г rfcp, а относительный сдвиг jf =

В В гФ = = f напряжение

у точки Bi будет:

. = Ot = rOg.

Найдём теперь напряжение Тр в какой-нибудь другой точке сечения Li, отстоящей от центра на расстоянии р (фиг. 125). Для

этого нужно найти величину относительного сдвига, который испытывает материал у точки Li. На фиг. 125 показан относительный сдвиг-г-угол перекоса LKLi, обозначенный ifp. Он будет меньше, чем относительный сдвиг на поверхности стержня. Повторяя те же рассуждения, что и при вычислении 7, мы г

найдём, что = Р , и получим: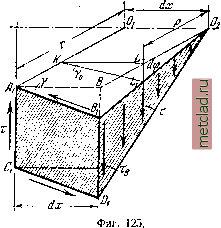

(11.6)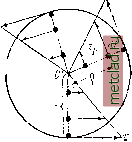

Относительный сдвиг и касательное напряжение в каждой точке поперечного сечения скручиваемого стержня прямо пропорциональны расстоянию р этой точки от центра сечения. Графически этот закон изменения касательных напряжений Фиг. 126. выражается прямой линией (фиг. 126).

Наибольшего значения т достигают в точках, лежащих у самого края сечения, и обращаются в нуль в центре.

Таким образом, найден закон распределения касательных напряжений но поперечным сечениям скручиваемого стержня.

\ pdF, т. е. сумма произведений из элементарных площадок на

квадраты расстояния их до точки О, называется полярным хмоменюм инерции и обозначается Jp, Тогда

откуда угол закручивания на единицу длины вала (относительный угол закручивания) равен:

=J (11.7)

Подставляя это в уравнение (11.6), получим:

.=р. (11.8)

Наибольшего значения напряжения достигнут в точках сечения

у поверхности вала при р = ртах =

Формулу для т,ах МОЖНО представить в ином виде:

(11.9)

(11.10)

Отношениеназывается моментом сопротивления при

Ртах

кручении; так как мо.мент инерции Jp выражается в единицах длины в четвёртой степени, то момент сопротивления Wp измеряется в единицах длины в третьей степени.

г. Величина касательных напряжений теперь может быть найдена из уравнения (11.5), выражающего условие равновесия отсечённой части.

Подставляя вместо Тр его значение (11.6) и вынося за знак интеграла величину О , постоянную при интегрировании по площади, получим: