§ 39]

НАХОЖДЕНИЕ НАИБОЛЬШИХ НАПРЯЖЕНИЙ

§ 39. Нахождение наибольших напряжений для объёмного напряжённого состояния.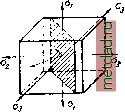

Для случая объёмного напряжённого состояния напряжения любой площадке можно представить также графически.

Пусть мы имеем выделенный из тела элемент кубической формы, на грани которого действуют три главных напряжения: Oi, о, <з (фпг. 87). Поставим задачу нахождения нормального и касательного напряжений по любой площадке, пересекающей выделенный кубик.

Сначала будем искать эти напряжения по площадкам, параллельным одному из главных напряжений, например а. На фиг. 87, а эта площадка заштрихована.

Как мы видели выше (§ 34), главное напряжение, параллельное проведённой площадке, не вызывает по ней ни нормальных, ни касательных напряжений. Поэтому напряжения по рассматриваемым площадкам будут зависеть лишь от (jg и <3з - для них мы будем иметь дело с плоским напряжённым состоянием. Тогда этим площадкам будут соответствовать точки круга напряжений, построенного на главных напряжениях и Og (фиг. 87,

Точно так же напряжения по площадкам, направленным параллельно ад, будут изображаться координатами то- .

чек круга, построенного на напряже-

ниях и Оз; для площадок, парал- Фпг. 87.

лельных Од, - на напряжениях и а.

Таким образом, координаты точек трёх кругов напряжений (фиг. 87, &) изображают нормальные и касательные напряжения по сечениям кубика, параллельным одному из главных напряжений.

Что же касается площадок, пересекающих все три оси главных напряжений, то в теории упругости показано, что для них напряжения о и т изображаются координатами точек D заштрихованной на фиг. 87, б площади.

Значения этих напряжений могут быть вычислены по формулам:

c = ai cosaj-f-a cosaa--a cos7.3, (7.15)

c = Ycl cos ai -- ai cos + a; cos-* аз - ol (7.16)

Здесь 1, a.2 и - углы, составленные нормалью к площадке направлениями соответствующих главных напряжений а, и а.

(7.17)

§ 40. Вычисление деформаций при плоском и объёмном напряжённом состояниях.

При проверках прочности элемента (фиг. 87), на грани которого действуют напряжения oj, а., аз, нам придётся столкнуться с вопросом о величинах соответствующих деформаций. Называя ребро, параллельное главному напряжению oj, первым, а рёбра, параллельные главным напряжениям и 03, вторым и третьим, определим относительные продольные деформации элемента в направлении этих рёбер, отдельно рассматривая влияние каждого из напряжений и складывая результаты.

Под действием напряжений oj элемент в направлении первого ребра получит относительное удлинение, равное

В то же время по отношению к напряжениям и первое ребро является поперечным размером, а потому под действием напряжений 02 и отдельно аз элемент в направлении первого ребра испытывает относительные укорочения, равные (см. § 9):

Полная относительная деформация элемента в направлешш первого ребра выразится суммой

I \ tf > > > Ci <Jo

Из фиг. 87 ясно, что в случае объёмного напряжённого состояния наибольшее и наименьшее нормальные напряжения равны соответственно наибольшему и наименьшему главным напряжениям.

Наибольшее касательное напряжение равно радиусу наибольшего круга, следовательно, полуразности наибольшего и наименьшего главных напряжений. Оно действует по площадкам, наклонённым под углом 45° к направлению этих главных напряжений, причём нормальные напряжения на таких площадках равны полусумме наибольшего и наименьшего главных напряжений (ojaag).

Таким образом, в общем случае напряжённого состояния материала, когда в рассматриваемой точке все три главных напряжения не равны нулю, получаем:

maxa - lf mina = 3*> max% ~ 2 (7-17)

По площадкам, параллельным одному из главных напряжений и наклонённым к двум другим на угол 45°, касательные напряжения будут: шах* по формуле (7.17), далее

- аз

§ 401

ВЫЧИСЛЕНИЕ ДЕФОРМАЦИЙ

Подобные же выражения получим и для деформаций в двух дру-гих направлениях; в результате имеем:

4 = --,i + -

(7.18)

Если какие-либо из напряжений а Og, будут сжимающими, то соответствующие числовые - значения их необходимо ввести в формулы (7.18) со знаком минус.

Из формулы (7.18) можно сейчас же получить выражения для случая растяжения или сжатия по двум направлениям, - тогда одно из главных напряжений следует положить равным нулю. Например, для случая, показанного на фиг. 81, имеем:

Ci а,

3 = -!-!--

(7.19)

Вычислим изменение объёма прямоугольного параллелепипеда со сторонами, равными а, 6 и с, в общем случае напряжённого состояния. До деформации объём его равен У = аЬс. После деформации, вследствие изменения длины рёбер, объём его станет

V, = {a + a){b + b)ic + cl

или, пренебрегая произведениями малых деформаций:

\\ = аЬс -аЬ C\-ac -j- Да = Vo (1 + + 2 + з)-

Относительное изменение объёма равно:

==-Ч + чЛ-Ч- (7.20)

Подставляя в эту формулу вместо е, sg, £3 их значения из формул (7.18), получим:

= 4 + 4 + 3 = --Ц (1 + а + з)-

(7.21)

Заметим, что если коэффициент Пуассона \х равен у, то отно-

шпельное изменение объёма равно нулю. Это мы уже получили § 9 для случая лг,нейного напряжённого состояния.