Следовательно,

/6 =

30 000

45 +

1 100

1250

- = 522,5 см\

Т. е. меньше, чем полученная в § 21 величина (605 слс).

Благодаря работам советских учёных проф. Лолейта, проф. Гвоздева и др. этот метод расчёта прежде, чем в других странах, был введён в СССР и принят некоторыми нашими нормами.

ГЛАВА VI.

УЧЁТ СОБСТВЕННОГО ВЕСА ПРИ РАСТЯЖЕНИИ И СЖАТИИ. РАСЧЁТ ГИБКИХ НИТЕЙ.

§ 29. Подбор сечений с учётом собственного веса (при растяжении и сжатии).

При установлении внешних сил, растягивающих или сжимающих элементы конструкций, мы до сих пор игнорировали собственный вес этих элементов. Возникает вопрос, не вносится ли этим упрощением расчёта слишком большая погрешность? В связи с этим

подсчитаем величины напряже-

б(х)

НИИ и деформаций при учёте влияния собственного веса растянутых или сжатых стержней.

Пусть вертикальный стержень (фиг. 60, а) закреплён своим верхним концом; к нижнему его концу подвешен груз А Длина стержня /, площадь поперечного сечения F, удельный вес материала 7 и модуль упругости Е. Подсчитаем напряжения по сечению АВ, расположенному на расстоянии X от свободного конца стержня.

Рассечём стержень сечением АВ и выделим нижнюю часть длиной X с приложенными к ней внешними силами (фиг. 60, б) - грузом Р и её собственным весом Fx. Эти две силы уравновешиваются напряжениями, действующими на площадь АВ от отброшенной части. Эти напряжения будут нормальными, равномерно распределёнными по сечению и направленными наружу от рассматриваемой части стержня, т. е. растягивающими. Величина их будет равна

Р б)

Фиг. 60.

(6.1)

§ 29] ПОДБОР СЕЧЕНИЙ С УЧЁТОМ СОБСТВЕННОГО ВЕСА 103

Таким образом, при учёте собственного веса нормальные напряжения оказываются неодинаковыми во всех сечениях. Наиболее напряжённым, опасныМу будет верхнее сечение, для которого х достигает наибольшего значения /; напряжение в нём равно

<Зтах = - + Т. (6.2)

Условие прочности должно быть выполнено именно для этого сечения:

/р \

- max -

+Tj<M. (6.3)

Отсюда необходимая площадь стержня равна

(6.4)

От формулы, определяющей площадь растянутого стержня без учета влияния собственного веса, эта формула отличается лишь тем, что из допускаемого напряжения вычитается величина f/.

Чтобы оценить значение этой поправки, подсчитаем её для двух случаев. Возьмём стержень из мягкой стали длиной 10 м\ для него а] = 1400 л;г/cл€ а величина 7/= 7,85 10 10 = 7,85 kzjcm. Таким образом, для стержня из мягкой стали поправка составит 7 85

т. е. ОКОЛО 0,бУо. Теперь возьмём кирпичный столб высотой

тоже 10 м\ ДЛЯ него [о] = 12 кг/сму а величина 7/== 1,8 10~ 10 = = 1,8 кг/см\ Таким образом, для кирпичного столба поправка

составит т. е. уже 15Vo-

Вполне понятно, что влиянием собственного веса при растяжении и сжатии стержней можно пренебрегать, если мы не имеем дела с длинными стержнями или со стержнями из материала, обладающего сравнительно небольшой прочностью (камень, кирпич) при достаточном весе. При расчёте длинных канатов подъёмников, различного рода длинных штанг и высоких каменных сооружений (башни маяков, опоры мостовых ферм) приходится вводить в расчёт и собственный вес конструкции.

В таких случаях возникает вопрос о целесообразной форме стержня. Если мы подберём сечение стержня (фиг. 60) по формуле (6.4) и дадим одну и ту же площадь поперечного сечения по всей длине, то материал стержня будет плохо использован; нормальное напряжение в нём дойдёт до допускаемого лишь в одном верхнем сечении; во всех прочих сечениях мы будем иметь запас в напряжениях, т. е. излишний материал. Поэтому желательно так запроектировать размеры стержня, чтобы во всех его поперечных сечениях (перпендикулярных к оси) нормальные напряжения были постоянны.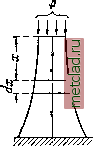

4F(x)dx dF(x) -

[о]. (6.5)

Отсюда

-J-dx

После интегрирования получаем

lnF(x) + C=x. (6.6)

Придг=0 площадь F(x) - Ff; подставляя эти значения в (б.б), имеем:

1по+С = 0 и С = -Ino-

Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.

Возьмём длинный стержень, подверженный сжатию силой Р и собственным весом (фиг. 61). Чем ближе к основанию стержня мы будем брать сечение, тем больше будет сила, вызывающая напряжения в этом сечении, тем ббльшими придётся брать размеры площади сечения. Стержень получит форму, расширяющуюся книзу. Площадь сечения F будет изменяться по высоте в зависимости от jc, т. е. F=f(x).

Установим этот закон изменения площади в зависимости от расстояния сечения х от \F{x}(iF{x) ggpg стержня.

Площадь верхнего сечения стержня F определится из условия прочности:

Фиг. 61. = W М

где [а] - допускаемое напряжение на сжатие; напряжения во всех прочих сечениях стержня также должны равняться величине

о = М = .

Чтобы выяснить закон изменения площадей по высоте стержня, возьмём два смежных бесконечно близких сечения на расстоянии х от верха стержня; расстояние между сечениями dx\ площадь верхнего назовём F(x)y площадь же смежного F (х)\-dF (х).

Приращение площади dF(x) при переходе от одного сечения к другому должно воспринять вес F{x)dx элемента стержня между сечениями. Так как на площади dF(x) он должен вызвать напряжение, равное допускаемому [о], то dF(x) определится из условия