= -; А = у; j; = asm-, 9г.2£У , Зг. . Зкх

(33.11)

Таким образом, чем больше точек перегиба будет иметь синусоидально-искривлённая ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (33.11), неустойчивы; они пе-

мым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sini/=0, и величина kl может иметь следующий бесконечный ряд значений:

/е/=0, г, 27:, Зтт, ... , nr., (33.7)

где п - любое целое число.

Отсюда А = , а так как =у то

- = j-.n и p=r. .n (33.8)

Иначе говоря, нагрузка, способная удержать слегка искривлённый стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять П = Пт[а.

Первый корень п = 0 требует, чтобы Р было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение п=1. Тогда получаем:

Рк = . (33.9)

(Здесь J-минимальный момент инерции поперечного сечения стержня.) Это - так называемая формула Эйлера для сжатого стержня с шарнирно-опёртыми концами. Значению критической силы (33.9) соответствует изгиб стержня по синусоиде с одной полуволной [формула (33.5)]

y = asm. (33.10)

Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (фиг. 554):

201]

ФОРМУЛА ЭЙЛЕРА ДЛЯ КРИТИЧЕСКОЙ СИЛЫ

реходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (фиг. 554).

Таким образом, поставленная задача решена; для нашего стержня наименьшая критическая снла определяется формулой

12 :

а изогнутая ось представляет синусоиду

y = asm -,

Величина постоянной интегрирования а осталась неопределённой; физическое значение её выяснится, если в уравнении синусоиды положить х = 1/2; тогда Ух=1/2 (т. е. посредине длины стержня) получит значение:

Значит, а - это прогиб стержня в сечении посредине его длины. Так как при критическом учении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения €ым1 малыми, то естественно, что прогиб / остался неопределённым.

Он должен быть при этом настолько малым, чтобы мы имели право применять приближённое -дафференциальное уравнение изогнутой оси, т. е.

/ \2

чтобы f -1 было мало по сравнению с единицей (18.5).

Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения а, разделив силу на плош.адь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для входит момент инерции Убр = бр> поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчёт полную, а не ослабленную, площадь поперечного сечения стержня F. Тогда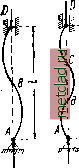

Фиг. 554.

т.ЕР

(33.12)

Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения.

Это отношение X = i называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.

Из формулы (32.12) видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность [а]. Так, для стали 3 с пределом прочности Од 4000 кг/см допускаемое напряжение может быть принято [а] =1600 кг/см; критическое же напряжение для стержня с гибкостью >ч=150 при модуле упругости материала iE = 2 10* кг/см будет равно

0 = (150)2= /ra/c.w<1600 кг/см.

Таким образом, если бы плош.адь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы.

§ 202. Влияние способа закрепления концов стержня.

Формула Эйлера была получена путём интегрирования приближённого дифференциального уравнения изогнутой оси стержня при \ff определённом закреплении его концов (шарнирно-опёр- i тых). Значит, найдетое выражение критической силы справедливо лишь для стержня с шарнирно-опёртыми концами и изменится при изменении условий закрепления концов стержня.

Закрепление сжатого стержня с шарнирно-опёртыми концами мы будем называть основным случаем закрепления. Другие виды закрепления будем приводить к основному случаю.

Если повторить весь ход вывода для стержня, жёстко заш.емлённого одним концом и нагружённого осевой сжимаюш.ей силой на другом конце (фиг. 555), то мы получим другое выражение для критической силы, а следовательно, и для критических напряжений.

Предоставляя учащимся проделать это во всех подробностях самостоятельно, подойдём к выяснению критической силы для этого случая путём следующих простых рассуждений.

Пусть при достижении силой Р критического зна-Фиг. 555. чения KOwTOHHa будет сохранять равновесие при слабом выпучивании по кривой АВ. Сравнивая фиг. 551 и 555, впдим, что изогнутая ось стержня, защемлённого одним концом, находится совершенно в тех же условиях, что и верхняя часть стержня двойной длины с шарнирно-закреплёнными концами.