§ 200] ПОРГЯТИЕ ОБ УСТОЙЧИВОСТИ ФОРМЫ СЖАТЫХ СТЕРЖНЕЙ 621

тическую, может происходить при непременном условии беспрепятственного возрастания искривления стержня; поэтому если при боковом выпучивании стержень встретит боковую опору, ограничивающую его дальнейшее искривление, то разрушение может и не наступить.

Обычно подобная возможность является исключением; поэтому практически следует считать критическую сжимающую силу низшим пределом разрушающей стержень силы.

Явление потери устойчивости при сжатии можно по аналогии иллюстрировать следующим примером из механики твёрдого тела (фиг. 552). Будем вкатывать цилиндр на наклонную плоскость аЬу которая потом переходит в короткую горизонтальную площадку be и наклонную плоскость обратного направления cd. Пока мы поднимаем цилиндр по плоскости аЬ, поддерживая его при помощи упора, перпендикулярного к наклонной плоскости, он будет Фиг. 552. в состоянии устойчивого равновесия; на

площадке Ьс его равновесие делается безразличным; стоит же нам поместить цилиндр в точку с, как его равновесие сделается неустойчивым- при малейшем толчке вправо цилиндр начнёт двигаться вниз.

Описанную выше физическую картину потери устойчивости сжатым стержнем легко осуществить в действительности в любой механической лаборатории на очень элементарной установке *). Это описание не является какой-то теоретической, идеализированной схемой, а отражает поведение реального стержня под действием сжимающих сил.

Потерю устойчивости прямолинейной формы сжатого стержня иногда называют продольным изгибом , так как она влечёт за собой значительное искривление стержня под действием продольных сил. Для проверки на устойчивость сохранился и до сих пор термин проверка на продольный изгиб , являющийся условным так как здесь речь должна итти не о проверке на изгиб, а о проверке на устойчивость прямолинейной формы стержня.

Установив понятие о критической силе как о разрушающей нагрузке, выводящей стержень из условий его нормальной работы, мы легко можем составить условие для проверки на устойчивость, аналогичное условию прочности.

Критическая сила вызывает в сжатом стержне напряжение,

называемое критическим напряжением и обозначаемое буквой р

0 = -. Критические напряжения являются опасными напряжениями для сжатого стержня. Поэтому, чтобы обеспечить устойчивость пря-

0 См. Н. М. Беляев, Лабораторные работы по сопротивлению материалов, § 85, Гостехиздат, 1951.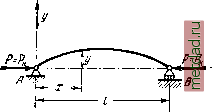

Фиг. 553.

МО линейной формы стержня, сжатого силами Р, необходимо к условию прочности (o = [afj добавить ещё условие устойчивости:

= Ы (33.1)

где [(Зу] - допускаемое напряжение на устойчивость, равное критическому, делённому на коэффициент запаса на устойчивость,

т. е. [.,]=.

Для возможности осуществить проверку на устойчивость мы должны показать, как определять и как выбрать коэффициент запаса ky,

§ 201. Формула Эйлера для критической силы.

Для нахождения критических напряжений надо вычислить критическую силу Ру т. е. наименьшую осевую сжимающую силу, способную удержать в равновесии слегка искривлённый сжатый стержень.

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.

Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует опреде- cZ лить, при каком значении осевой сжимающей силы Р такое искривление возможно.

Рассмотрим прямой стержень постоянного сечения, шарнирно опёртый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (фиг. 553). Собственным весом стержня пренебрегаем.

Нагрузим стержень центрально приложенными продольными сжимающими силами Р=Р и дадим ему весьма небольшое искривление в плоскости наименьшей жёсткости; стержень удерживается в искривлённом состоянии, что возможно, так как Р = Р,

Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближённым дифференциальным уравнением изогнутой оси стержня (§ 109). Выбрав начало координат в точке А и направление координатных осей, как показано на фиг. 553, имеем (18.7):

§ 201] ФОРМУЛА ЭЙЛЕРА ДЛЯ КРИТИЧЕСКОЙ СИЛЫ 623

Возьмём сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у у а изгибающий момент равен

Ж(лг) = -Ру.

По схеме, изображённой на фиг. 499, изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, г у - отрицательным и М(х) - - Ру.)

Приведённое только что дифференциальное уравнение (18.7) принимает вид:

EJ% = -Py\ (33.2)

деля обе части уравнения на EJ и обозначая дробь через /г приводим его к виду:

g + *!v = 0. (33.3)

Общий интеграл этого уравнения имеет вид:

y - a%\nkx-\-b cos kx, (33.4)

Это решение заключает в себе три неизвестных: постоянные интегрирования а и и значение =/ > так как величина критической силы нам неизвестна.

Условия на концах стержня дают два уравнения:

в точке А при х = 0 прогиб j; = О, В х = 1 у - О.

Из первого условия следует (так как %\nkx - 0 и zosky=\)

0 = b.

Таким образом, изогнутая ось является синусоидой с уравнением

y = asinkx. (33.5)

Применяя второе условие, подставляем в это уравнение

у = 0 и х = 1;

получаем:

0 = asin W. (33.6)

Отсюда следует, что или а или И равны нулю.

Если а равно нулю, то из уравнения (33.5) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался пря-