§ 198] НАПРЯЖЕНИЯ в СФЕРИЧЕСКИХ ТОЛСТОСТЕННЫХ СОСУДАХ 615

Минимальная температура до которой надо нагреть наружный цилиндр при надевании его на внутренний, определяется уравнением

отсюда

(при наших числовых данных: а = 125 10~; Е= 2 10* кг/см*; Arf = 0,0137 см).

§ 198. Напряжения в сферических толстостенных сосудах.

На фиг. 547 изображён элемент, вырезанный из толщи стенки толстостенного сферического сосуда; внутренний радиус этого элемента равен г, а наружный г+П напряжения, действующие на этот элемент, изображены на чертеже. Составляя уравнения равновесия и совместности, получаем для и значения:

А .

(32.12)

Постоянные А и В могут быть определены из условий на внутренней и внешней поверхностях сосуда при

г = Гг и г = Г1

соответственно, где п и Гг -наружный и внутренний радиусы.

Так, при действии внешнего pi и внутреннего р давлений А п В определяются Фиг. 547. из условий:

= Л + -у = - ps на внутренней поверхности, В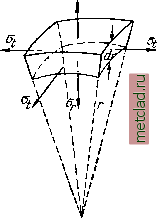

= Л + = - Pi внешней поверхности.

Отсюда

Тогда

Pin-Pin

(32.13)

§ 199. Расчёт тонкостенных сосудов.

Если толщина стенок цилиндра t = ri - ri мала по сравнению с радиусами Г1 и Гг, то из формулы (32.10) мы получаем:

Р2Г

т. е. величину, определённую нами раньше (§ 34).

Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределённым симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.

Выделим (фиг. 548) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными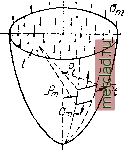

(JmdSft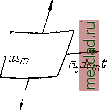

Фиг. 548.

к меридиану. Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно dZj и йц, радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим и Р толщину стенки назовём t.

По симметрии по граням выделенного элемента будут действовать только нормальные напряжения в меридиальном направлении и в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут mt и tm- Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.

Усилия adSmt = ac = bc (фиг. 549) дадут в нормальном к поверхности эле-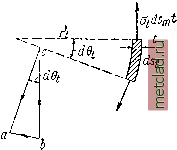

Фиг. 549.

мента направлении равнодействующую аЬ, равную

abTcdbiOidSmt Подобным же образом усилия fst дадут в том же направлении равнодей-

ствующую <mdSidSm-* Сумма этих усилий уравновешивает нормальное дав-ление, приложенное к элементу

Р dSmdSt = mdStdSm + dSmdSt -f .

9m Pt

Отсюда

(32.14)

Это основное уравнение, связывающее напряжения и для тонкостенных сосудов вращения, дано Лапласом.

Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.

Рассмотрим случай гидростатической нагрузки (фиг. 550). Меридиональную кривую отнесём к осям х \l у z началом координат в вершине кривой. Сечение проведём на уровне у от точки О, Радиус соответствующего параллельного круга будет x.

Каждая пара усилий mdtt, действующих на диаметрально противоположные элементы dst проведённого сечения, даёт вертикальную равнодействующую Ьс равную

be - 2ab cos 0 = 2а dstt cos 0;

сумма этих усилий, действующих по всей окружности проведённого сечения, будет равна 2Tzx(ijnt cos 0; она будет уравновешивать давление жидкости p=zf(h-у) на этом уровне плюс вес жидкости в отрезанной части сосуда Ру

Отсюда

27СХС COS 0 = КХр -f Ру,

2t cos 6

2Tzxt COS e

(32.15)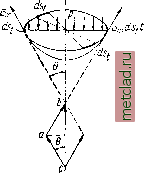

Фиг. 550.

Зная уравнение меридиональной кривой, можно найти X vi Ру для каждого значения у, и стало быть, найти а, а из уравнения (32.14) и

Например, для конического резервуара с углом при вершине *а, наполненного жидкостью с объёмным весом y на высоту /г, будем иметь:

Р;;, = оо; xy\ga\ Р, = у Т.Д=-i-ТтУ tg2 а;

COSa