§ 17.8]

ВЫЧИСЛЕНИЕ КАСАТЕЛЬНЫХ НАПРЯЖЕНИЙ

§ 178. Вычисление касательных напряжений в сечении тонкостенного стержня.

Теперь, когда все силовые факторы определены, остаётся произвести вычисление касательных напряжений, возникаюпдих в сечении стержня под действием внешнего крутящего момента Л1ф = Л1, + Ж,.

О касательных напряжениях от чистого кручения уже было сказано в §§ 173, 176 и 67 [формулы (11.37)]. Для определения

секториальных касательных на-

пряжений воспользуемся той - f /Л:>2 же методикой, какая была принята при выводе формулы Журавского (§ 91).

Вырежем из рассматриваемого стержня (фиг. 467) элемент длиной dXy одна из граней которого (например, нижняя) свободна от касательных напряжений (фиг. 483). Элемент находится в равновесии под действием секториальных

нормальных и касательных напряжений. Обозначим нормальные напряжения, действующие на левую грань 7-7 и на правую 2-2 соответственно;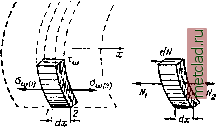

Фиг. 483.

а>(1)-

И о.

По этим же граням действуют секториальные касательные напря-жения т. По закону парности касательные напряжения действуют также по площадке, параллельной оси jc. Эти касательные напряжения должны сложиться в усилие, уравновешивающее разность нормальных усилий, действующих в сечениях 1-1 и 2-2 по торцевым площадкам отсечённого элемента.

Величины нормальных усилий соответственно равны:

отс отс

с (odf п

dF и N.

B+dB

idF.

Так как интеграл

редставляет собой секториальный стати-

ческий момент отсечённой площади торца элемента [см, формулу (30.14)], то

а сдвигающая сила, уравновешиваемая секториальными касательными напряжениями, равна:

dN=N.2 - N, = -jSL

♦со

Отсюда величина искомых секториальных касательных напряжений будет:

dN dB

dxb dxbJ,/

Имея в виду, что - = М (30.24), получим:

(30.32)

Структура полученной формулы совершенно аналогична структуре формулы Журавского для вычисления касательных напряжений при поперечном изгибе. Заметим, что величина секториальных касательных напряжений сравнительно невелика. Однако, несмотря на это, они принимают на себя значительную долю внешнего момента, так как плечи соответствующих касательных усилий обычно велики (см., например, фиг. 466, б),

В формулы для секториальных напряжений (30.19) и (30.32) входят секториальные координаты и новые секториальные геометрические характеристики сечения, методы определения которых приводятся ниже (см. §§ 179 и 180).

§ 179. Вычисление секториальных площадей. Построение секториальных эпюр.

Выше было показано, что секториальная площадь равна (30.7):

где г - перпендикуляр, опущенный из полюса А на направление касательной к средней линии сечения, проведённой через данную

точку (фиг. 484). Пределы интегрирования определяются выбором начала координат, т. е. того луча AM, от которого ведутся отсчёты. Точка Ж, лежащая на средней линии сечения, называется началом отсчёта.

Как известно (§ 174), интеграл J равен удвоен-

ной площади заштрихованного на фиг. 484, а сектора, ограниченного лучами AM, An и контуром средней линии сечения. Для контура,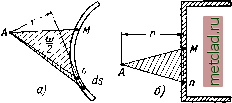

Фиг. 484.

§ 179]

ВЫЧИСЛЕНИЕ СЕКТОРИАЛЬНЫХ ПЛОЩАДЕЙ

ограниченного прямыми линиями, секториальная площадь равна удвоенной площади треугольника, заключённого между линией контура и лучами AM и An (фиг. 484, б).

Нетрудно видеть, что каждой точке сечения соответствует своя секториальная площадь. Поэтому секториальную площадь можно рассматривать как секториальную координату данной точки.

Если вычислять значения секториальных площадей для каждой точки сечения и откладывать их в определённом масштабе по нормали к средней линии сечения, то мы получим так называемую эпюру секториальных площадей, т. е. график, показывающий закон изменения о) по контуру сечения.

При криволинейном контуре сечения длина перпендикуляра г, а значит и величина секториальных площадей о), изменяется по длине контура, в зависимости от его очертания [а)==а)(5)]. В этом случае эпюра секториальных площадей будет криволинейной.

Если контур сечения представляет собой ломаную линию, то для всех точек каждого прямолинейного участка величина, г будет иметь одно и то же значение и эпюра секториальных координат (фиг. 484, б) будет состоять из отдельных прямолинейных участков.

Условимся о знаках. Знак секториальной координаты о) для некоторой точки п считаем положительным, если подвижной радиус-вектор при переходе от выбранного начального радиуса AM в положение An поворачивается по часовой, стрелке (фиг. 485, а). В обратном случае величина w считается отрицательной (фиг. 485, б). Если радиус-вектор пересекает контур сечения, то секториальная площадь определяется как алгебраическая сумма двух площадей разных знаков (фиг. 485, в):

О) = - т\Ь-\- га = - (*>1 --

Как это видно из сопоставления чертежей (фиг. 485, а и фиг. 485, г), если начало отсчётов взять не в точке Л4, а в другой какой-нибудь точке Жх, то секториальная площадь (координата) для той же точки получит другое значение и по величине, и по знаку.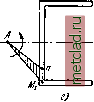

Фиг. 485.

Нетрудно видеть, что величина секториальной площади зависит также и от положения полюса А, из которого ведётся построение.