щий величину момента инерции при изгибе балки. Полученный новый интеграл, т. е. сумма произведений из элементарных площадок на квадраты их секториальных координат называется секториаль-ным моментом инерции сечения и обозначается J.

Следовательно, изгибно-крутя-Ш.ИЙ бимомент равен:

(30.18)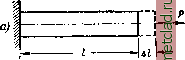

Подставив теперь в выражение (30.10) ~ вместо -£6 , найдём:

(30.19)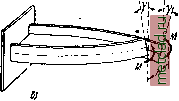

Фиг. 473.

Полученная формула по своему виду совершенно аналогична формуле для нормальных напряжений

рри изгибе (о = ]. Таким обра-

\ Jy J

зом, для вычисления секториальных Напряжений необходимо изучить методы вычисления величин, входящих в формулу (30.19): изгибно-крутящего бимомента i5, секториального момента инерции и секториальных координат со.

В целях развития представления об изгибно-крутящем бимоменте, рассмотрим один приём вычисления внешних бимоментов i), Пусть мы имеем в плоскости zOy ломаный стержень АБСу защемлённый одним концом, к другому концу которого приложена liapa сил, лежащая в некоторой плоскости, параллельной оси х (фиг. 474).

Взяв сечение в расстоянии у от начала координат, приложим в точке А две равные и противоположно направленные пары Жо (в плоскости, параллельной заданной паре). В результате переноса пары в точку А мы получили пару заданного направления и совокупность двух проти1воположных пар Ж© с расстоянием г между плоскостями их действия, т. е. бипару с бимоментом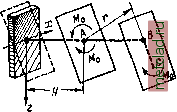

Фиг. 474.

(30.20)

О См. Б ы ч к о в д. в.. Расчёт рам, Стройиздат, 1948; П р а т у с е в и ч Я. А., Вариационные методы в строительной механике, ГТТИ, 1948.

Если к свободному концу того же стержня приложена не пара сил, а сила Р, перпендикулярная к плоскости ABC (фиг. 475), то, перенеся силу в точку fi, получим силу и пару сил с моментом М = Ре,

Опустив теперь из некоторой точки А перпендикуляр г на плоскость этой пары, получим (в соответствии с формулой (30.20)) значение изгибно-крутящего бимомента (момента бипары):

В = М-г = Рег, (30.20)

Таким образом, изгибно-крутящий бимомент В относительно точки А есть произведение изгибно-крутящей пары Ре на плечо -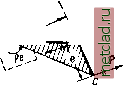

Фиг. 475.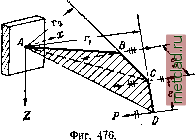

перпендикуляр г, опущенный из точки А на плоскость этой пары. Выражение (30.20) можно представить и в другой форме. Как видно

из чертежа, произведение ег представляет собой удвоенную площадь тре-В угольника ABC. Обозначим эту площадь через О). Тогда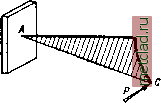

В = Рт.

(30.21)

Для ломаного стержня, состоящего из Фиг. 477. трёх прямых отрезков, изображённого на

фиг. 476, после переноса силы в точки В и О получим величину бимомента как сумму бимоментов двух пар Mi = Pei (перечёркнута двумя чёрточками) и М = Ре2 (перечёркнута тремя чёрточками):

В = Mifi -f ЖаГз = Peifi -j- Ре = Р (eri + er).

Но iri = o)j, т. е. удвоенной площади треугольника ACD, а ег - удвоенной площади треугольника ABC и, окончательно,

Б = р (0)14- щ) = Ро), (30.22)

где О) - удвоенная площадь, заштрихованная на фиг. 476 *).

1) Формулой (30.22) можно пользоваться для определения внешних изгибно-крутящих бимоментов лишь в случаях, когда жёсткостью стержня при кручении можно пренебречь (см. § 177).

Если плоский стержень имеет вид, показанный на фиг. 477, то очевидно, что изгибно-крутящий бимомент, соответствующий действию приложенной СИЛЫ Я, будет равен:

В = РС1),

где а> - удвоенная заштрихованная площадь ABC.

Для перехода к вычислениям внешних изгибно-крутящих бимо-ментов в тонкостенном стержне представим себе, что ломаные линии, рассмотренные выше (фиг. 474-477), изображают собой не ось стержня, а среднюю линию его поперечного сечения, связанную с полюсом А, а также, что точка Л, в которую производился перенос сил, является центром изгиба сечения. В таком случае ш - это та же секто-риальная площадь, о которой шла речь в § 174. Действительно, если в некоторой точке п поперечного сечения стержня (фиг. 478) приложено усилие dP=ajlF, то после переноса его в точку My оно приводится к силе dP = oJiF и паре сил

dM = dPS=odFS.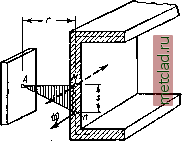

Фиг. 478.

Опустив из точки А перпендикуляр на плоскость этой пары, получим, в соответствии с формулой (30.20), изгибно-крутящий бимомент

dB - dMr = odF * 8Г\

здесь 5 г (удвоенная площадь треугольника АМп) и, следовательно:

dB-cdF чл.

Тогда величина изгибно-крутящего бимомента, действующего в сечении, будет

. О) dF,

Фиг. 479.

что совпадает с формулой (30.17), полученной из других соображений.

Бимомент иногда обозначаюТ как показано на фиг. 479. Условимся относительно знака бимомента. Изгибно-крутящий бимомент будем считать положительным, если при взгляде со стороны полюса А вдоль радиуса г мы видим, что изгибно-крутящая пара вращает против часовой стрелки. В соответствии с этим на фиг. 478 бимомент положителен, а на фиг. 477 - отрицателен.