§ 174. Деформация тонкостенного стержня, связанная С неравномерной депланацией сечений.

В предыдущем параграфе было показано, что задача определения .напряжений в сечениях тонкостенного стержня при стеснённом кру-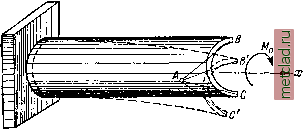

Фиг. 467.

чении статически неопределима. Для раскрытия статической неопределимости рассмотрим деформацию тонкостенного стержня с открытым сечением произвольной формы, контур которого очерчен кривыми линиями (фиг. 467). КоН туры поперечных сечений считаем недеформируемыми (см. § 173) в своей плоскости, а сечения, не остающимися плоскими.

Теоретические выводы о деформации тонкостенного стержня, рассматриваемые ниже, хорошо согласуются с данными опытов.

Пусть к свободному концу тонкостенного стержня, защемлённого одним концом, приложен момент Жо, вызывающий изгибное кручение (фиг. 467). Так как стержень взят несимметричного профиля, то повороты сечений происходят вокруг их

центров изгиба А. При повороте произвольного сечения на угол db и депланации его точка /г, принадлежащая любому продольному волокну, перемещается в новое положение Пу (фиг. 468, 469) ). Это перемещение

О Вследствие малой толщины стенок профиля можно считать, что интересующие нас продольные перемещения и соответствующие им нормальные Напряжения по толщине стенки одинаковы. Поэтому можно ограничиться рассмотрением деформаций волокон серединной поверхности.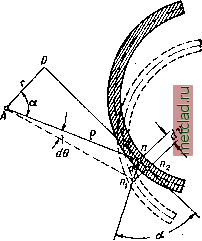

Фиг. 468.

МОЖНО рассматривать как состоящее из трех составляющих: одной - вдоль касательной к серединной линии сечения в точке /I, (п - п), второй - вдоль образующей (перпендикулярной к плоскости чертежа и потому на фиг. 468 невидимой) и третьей - {п< - /,), перпендикулярной к касательной п - /г; последняя нас не интересует, так как мы ищем удлинение волокна (вдоль образующей), связанное с депла-нацией сечения.

Сначала определим тангенциальную составляющую перемещения {п - щ), а затем продольную, которую можно связать с тангенциальной. Для определения тангенциальной составляющей перемещения воспользуемся гипотезой о недеформируемости контура сечения. На основании этой гипотезы, при определении касательного перемещения, лежащего в плоскости сечения, можно рассматривать перемещение сечения в новое положение как поворот жесткого диска вокруг центра изгиба (точка А на фиг. 468 и 469), лежащего в плоскости сечения.

Ограничимся рассмотрением поворота на бесконечно малый угол dB, считая его за угол поворота одного сечения относительно другого, смежного с ним, отстоящего на расстояние dx. При этом повороте точка п опишет радиусом р дугу п - л, равную a = pdB.

Опустив перпендикуляр r - AD из точки А на продолжение касательной nDt получим при вершине А угол а, равный углу между сторонами п - щ и п - треугольника щт. Перемещение п - щ по касательной равно

dv = a cos а.

Фиг. 469.

Имея в виду, что г= р cos а, получим:

dv = pdB cos а = г db.

(30.5)

Перейдем к отысканию продольной составляющей перемещения, которую обозначим du. Рассмотрим два бесконечно близких сечения ВС и DE с расстоянием между ними dx (фиг. 469).

При повороте сечения ВС относительно DE на угол db и переходе точки п в новое положение щ образующая kn повернётся на угол Y, равный, как видно из чертежа.

Знак минус взят потому, что отрицательному направлению угла db (если смотреть от начала координат вдоль оси х - против часовой

стрелки) соответствует положительный угол (по часовой стрелке, если смотреть от полюса вдоль радиуса г), и наоборот (фиг. 469 - 470).

Выделим на серединной поверхности стержня около рассматриваемой точки п элементарный квадрат, одна из сторон которого является элементом дуги ds (фиг. 470). На основании гипотезы об отсутствии сдвигов на серединной поверхности этот квадрат при перемещении точки п в новое положение щ не перекосится, прямые углы его останутся прямыми. Вследствие этого элемент дуги ds выйдет из плоскости поперечного сечения. Нижний конец элемента ds сместится вдоль оси стержня относительно верхнего на величину:

du = ds* sin Y flf5 Y.

Фиг. 470.

Подставляя вместо y его значение, найдём элементарное продольное перемещение:

du = -ds.r.

Полное перемещение, накопленное как сумма перемещений на элементарных отрезках rfs, будет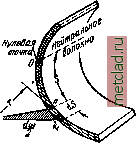

Здесь г - перпендикуляр, опущенный из центра изгиба А на направление касательной к серединной линии сечения, проведённой через рассматриваемую точку п. Нетрудно видеть (фиг. 471), что произведение rds равно удвоенной площади заштрихованного треугольника Anki с основанием dSy которую обозначим flfa) = 2 пл. Д Anki. Суммируя эти элементарные площади по длине дуги s, найдём некоторую удвоенную площадь:

y=rds. (30.7)

<Й1Г. 471.

Эта площадь названа секториальной площадью или секториаль-Цой координатой точки л, соответствующей дуге длиной 5, отсчитываемой от главной нулевой точки, для которой а)о = 0. Методы вычисления секториальных площадей для различных сечений приведены ниже (§ 179).