Таким образом в результате переноса сил мы можем заменить систему внешних сил Р, действующую на оставленную левую часть бруса, статически эквивалентной ей системой из шести составляющих: трёх сил, приложенных к центру тяжести выбранного сечения и направленных вдоль координатных осей, и трёх моментов, действующих вокруг этих же осей.

Из предыдущего известно, какое действие на левую часть бруса оказывает каждая из этих шести составляющих. В рассматриваемом сечении положительная составляющая У?р(=ЛО - нормальная сила - вызывает сжатие левой части бруса; изгибающий момент My и поперечная сила Q;f{=Rz)- соответственно изгиб и сдвиг бруса в плоскости xz; изгибающий момент М и поперечная сила Qy (= Л у) - изгиб и сдвиг в плоскости ху; момент М вызывает кручение бруса вокруг оси х.

Таким образом, в самом общем случае действия сил на брус в нём возникают четыре простых деформации: осевое растяжение -или сжатие, два плоских изгиба и кручение.

Б. Составим формулы для вычисления нормальных и касательных напряжений в какой-либо точке А с координатами у п z, расположенной в первом квадранте сечения тп (фиг. 453). При этом будем считать, что все шесть составляющих системы внешних сил являются положительными (фиг. 452). В се- Фиг. 453. чении тп возникают уравновешиваю-щие эту систему нормальные и касательные напряжения. Нормальные напряжения обусловлены действием продольной силы ЛГ и изгибающих моментов My и Mg. От положительной про-, дольной силы N возникают уравновешивающие её равномерно распределён-

ные по сечению сжимающие напряжения в = - (фиг. 453). Положительные изгибающие моменты М и соответственно уравновешиваются нормальными напряжениями а и о ; при этом от положительного момента My в точке А возникает сжимающее напряжение o =s - У-, а от положитель-

ного момента М - растягивающее напряжение от = -f--j,

Суммируя эти составляющие нормального напряжения, получаем такую формулу для вычисления полного нормального напряжения в точке А: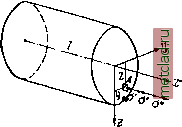

or = ff -j- ff 4- a = - -vr--f- + -

r Jy

(29.1)

Для вычисления полного нормального напряжения в любой другой точке поперечного сечения бруса достаточно подставить в формулу (29.1) значения N, My и Mg а также и координат > и 2, с их знаками; при этом мы всегда будем получать надлежащие величину и знак полного нормального напряжения.

Полагая в формуле (29.1) напряжение сг равным нулю и обозначая координаты точек нулевой линии через у и г©, для нахождения положения этой линии получаем такое уравнение: >

Отрезки, отсекаемые нулевой линией на осях координат у и соответственно равны (фиг. 454):

J, N N

(29.2)

Тангенс угла наклона (Р) нейтральной линии к оси у равен:

(29.3)

Нейтральная линия в общем случае делит поперечное сечение бруса на две области: растянутую и сжатую (фиг. 454). Проводя линии, параллельные нейтральной и касательные к контуру поперечного сечения, находим в той и другой области наиболее удалённые от нейтральной линии точки / и 2

с наибольшими растягивающими и сжимающими напряжениями. Подставляя координаты этих точек (ух и 21 или у и 2:2) с ИХ знаками в формулу (29.1), находим наибольшие значения растягивающих, и сжимающих напряжений: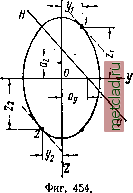

1,2) =

TV F

(29.4)

Касательные напряжения в сечении тп возникают вследствие кручения бруса вокруг оси х и сдвига его в плоскостях ху и xz.

Крутящий момент уравновешивается касательными напряжениями т. Для бруса с поперечным сечением в виде круга или кольца эти напряжения вычисляются (§ 57) по формуле:

(29.5)

Для брусьев с поперечным сечением любой другой формы должна быть использована формула, приведённая в § 67 (таблица 17):

шах к

(29.6)

Во всех случаях наибольшие касательные напряжения возникают на контуре поперечного сечения и направлены вдоль касательной к контуру.

Касательные напряжения от сдвига, уравновешивающие силы и 0, как правило, играют второстепенную роль; они находятся по формулам (§ 91):

Q.S(z)

QySiy) JzHy)

Jyb{z)-

(29.7)

Для прямоугольного и круглого сечений касательные напряжения (29.7) достигают максимума на соответствующих главных осях инерции: ty - на оси 2, а - на оси у. Суммарные касательные напряжения от двух плоских изгибов наибольшего значения достигают в центре тяжести сечения, т. е. как раз там, где касательные напряжения от кручения и нормальные напряжения от изгиба равны нулю. Благодаря этому определение этих напряжений часто не имеет практического значения.

В связи с тем, что нормальные напряжения от изгиба и касательные напряжения от кручения наибольших значений достигают на контуре поперечного сечения, именно там обычно приходится искать наиболее напряжён-

С Mldx г Ml d>

в связи с этим формула (29.8) получает теперь такой вид:

2EF2GJ2EJy 2EJg

dx. (29.9)

Значок / показывает, что интегрирование распространяется на длину такого участка бруса, на протяжении которого функции координаты х, т. е. Л, Мх,

ные точки и производить проверку прочности материала бруса. Точки с наибольшими касательными напряжениями не всегда совпадают с точками, в которых возникают наибольшие нормальные напряжения. Поэтому в наиболее тяжёлых условиях материал бруса находится у тех точек контура, в которых получается наиболее неблагоприятное сочетание нормальных и касательных напряжений. Такими точками могут быть: точки с наибольшими нормальными напряжениями, точки с наибольшими касательными напряжениями и какие-либо промежуточные точки контура сечения. В случае надобности могут быть учтены также и касательные напряжения от изгиба; тогда полное касательное напряжение должно быть найдено путём геометрического суммирования т, и V

Для проверки прочности материала в самом общем случае действия сил на брус должны быть использованы расчётные формулы § 94 [формулы (15.14-15.17)] или § 167 [формулы (28.1)], выведенные на основе той или иной теории прочности. Сравнивая величину расчётного напряжения, вычисленного по одной из формул (15.14-15.17) или (28.1), с величиной допускаемого напряжения, получаем возможность решить одну из двух практически важных задач: определить размеры поперечного сечения бруса или проверить прочность материала при известных размерах сечения бруса.

В. Для вычисления перемещений призматического бруса, *нагружённого системой сил, как угодно расположенных в пространстве, применяем принцип независимости действия сил (ограничение см. § 161). Это может быть выполнено с помощью приёмов, изложенных ранее в соответствующих разделах курса.

Не останавливаясь на других приёмах, напомним использование теоремы Кастильяно (§ 126). Потенциальную энергию деформации при сложном сопротивлении рассматриваемого здесь бруса можно представить в виде суммы количеств энергий от всех шести составляющих: Qy, Qg, М My и Mg, Пренебрегая энергией касательных напряжений от изгиба, имеем:

UU{N) + U{M) + U {My) + и {Mg). (29.8)

Полагая, что нормальное усилие N и крутящи момент Мх в общем случае не остаются постоянными на протяжении всей длины бруса, для энергии в элементе бруса длиной dx следует написать такие выражения:

Л72 Ах М\, dx

а для энергии на участке бруса длиной /:

С Ndx С М. dx

W (>=)-

Для энергии нормальных напряжений при плоском изгибе соответственно имеем (§ 125):

Mldx