ОТДЕЛ VIH.

СЛОЖНОЕ СОПРОТИВЛЕНИЕ.

ГЛАВА XXVI. КОСОЙ ИЗГИБ.

§ 156. Основные понятия.

До сих пор мы рассматривали задачи, где стержни конструкции испытывали одну из простейших деформаций: осевое растяжение или сжатие, кручение, плоский изгиб. На практике же большинство элементов конструкций и машин подвергается действиям сил, вызывающих одновременно не одну из указанных деформаций, а две и более.

Валы машин подвергаются действию кручения и изгиба; стержни ферм (стропильных, мостовых, крановых), помимо растяжения или сжатия, испытывают ещё и изгиб, вызываемый устройством в узлах сварных или клёпаных соединений взамен шарниров, предполагающихся при выполнении расчётов. Все такие случаи сопротивления стержней, когда мы имеем дело с комбинацией простейших деформаций, называются сложным сопротивлением.

При расчётах на сложное сопротивление обычно исходят из так называемого принципа независимости действия сил, т. е. предполагают, что влиянием деформаций, вызванных одной из приложенных к упругой системе нагрузок, на расположение, а следовательно, и на результаты действия остальных нагрузок можно пренебречь. Опыт показывает, что пока деформации системы малы этот принцип может быть использован (исключительные случаи, когда он вообще не применим, будут рассмотрены ниже); а поэтому для нахождения полных напряжений и деформаций, возникающих в упругой системе в результате действия на неё любой сложной системы нагрузок, можно применять способ сложения действия сил, т. е. геометрически суммировать напряжения и перемещения, соответствующие различным видам простейших деформаций.

Вначале рассмотрим решение частных задач сложного сопротивления, а затем и самый общий случай действия сил на упругую систему.

§ 157. Косой изгиб. Вычисление напряжений.

Для вычисления нормальных напряжений при изгибе мы до сих

ор пользовались формулой: а = -у-. Однако нормальные напряже-

ия в каком-либо сечении балки полностью определяются по этой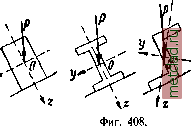

ются нагрузкам,

формуле только в случае плоского изгиба когда искривление оси балки происходит в плоскости действия сил и нейтральной осью является главная ось инерции поперечного сечения, перпендикулярная к плоскости нагрузки.

На практике часто встречаются случаи, когда плоскость действия сил, перпендикулярных оси стержня, не совпадает ни с одной из двух плоскостей, проходящих через ось стержня и главные оси инерции поперечных сече- 1 НИИ стержня. Опыт по-

> \ У казывает, что изогну-

тая ось стержня при этом уже не будет лежать в плоскости действия сил, и мы будем иметь случай так называемого косого изгиба. Обрешетины кровли обычно подверга-плоскость действия которых составляет довольно значительный угол с главными осями (фиг. 408); довольно часто встречаются И случаи, когда направление нагрузок лишь слегка отклоняется от главных осей инерции.

Покажем на примере метод проверки прочности и вычисления деформаций балок при косом изгибе.

Рассмотрим балку у защемлённую одним концом и нагружённую на другом силой лежащей в плоскости торца балки и направленной под углом ср к главной оси Bz (фиг. 409). Вторая главная ось By пойдёт перпендикулярно к первой; направления этих осей выберем так, чтобы сила Р проходила в первом квадранте координатной системы.

Для проверки прочности необходимо найти точку с наибольшим нормальным напряжением. Выведем сначала формулу для вычисления

) Говоря более точно, это будет иметь место, когда все силы лежат в одной из главных плоскостей инерции стержня, проходящей через центр изгиба; в целом ряде случаев последний совпадает с центром тяжести поперечного сечения (§ 96).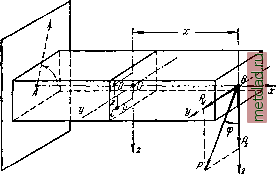

Фиг. 409.

нормального напряжения в любой точке произвольного сечения, отстоящего в расстоянии х от свободного конца балки.

Разложим силу Р на составляющие Р и Ру, направленные по главным осям инерции сечения Bz и By. Величины этих составляющих определяются формулами

= Я cos ср и Ру = Р sin ф.

Таким образом, мы привели случай косого изгиба к комбинации двух плоских изгибов, вызванных силами Р и Ру, расположенными в главных плоскостях инерции балки. Суммируя напряжения и деформации, соответствующие каждому из этих изгибов, мы получим решение и для косого изгиба.

Изгибающие мОхменты в сечении с абсциссой х от сил Р и Р будут равны

Ж, = Рл: = Р;со$ср = Жсо8ср, \

\N[z\ = PyX = PX %т-=ЛЛът. J

Значки у \А Z при М обозначают главные оси, относительно которых берутся моменты; буквой Ж обозначен изгибающий момент в плоскости действия силы Р, для проведённого сечения равный Рх. Применяя векторное изображение моментов, видим, что для вычисления изгибающих моментов 1Ау и можно было непосредственно разложить полный изгибающий момент Ж по главным осям (фиг. 410).

Для установления знаков изгибающих моментов следовало бы ввести дополнительные условия, определяющие эти знаки в связи с переходом к пространственной задаче. Это и будет сделано ниже; сейчас же ограничимся лишь вычислением абсолютной величины изгибающих моментов, влияние же направления моментов на знаки напряжений учтём при вычислении последних.

Вычислим напряжения в какой-либо точке С (с координатами у и г), расположенной в первом квадранте (фиг. 409). Мы имеем возможность вычислить для этой точки нормальные напряжения, вызванные отдельно моментами My и Л4, изгибающими балку в главных плоскостях XZ и ху\ в этом случае применимы формулы, полу-сенные для плоского изгиба.

Нормальное напряжение в точке С от изгиба моментом М, является сжимающим (отрицательным) и выражается формулой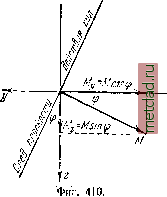