Далее решение не отличается от описанного в способе сравнения деформаций.

Раскрытие статической неопределимости возможно выполнить также и по теореме Мора. При решении по Мору, кроме первого состояния нагружения основной балки заданной нагрузкой и лишней неизвестной силой (фиг. 362, а)у следует показать ту же балку во втором состоянии загружения - силой Р=1 (фиг. 362, б).

P-f Вычисления при обозначениях, принятых на фиг. 362, дают:

М = + Бх-Щ;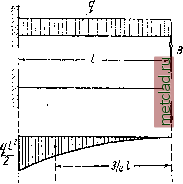

М tllllliillW

Фиг. 362.

yVl = + JC,

Величина момептных площадей:

т. е. то же, что и при пользовании теоремой Кастильяно (23.6). 2) При решении того же примера по способу Верещагина к двум схемам состояний загружения (фиг. 362, а и б) следует а построить эпюры моментов: от нагрузки q (фиг. 362, в), от силы В (фиг. 362, г) и от силы Р =1 (фиг. 362, д).

от нагрузки q: со

~ 3 2

ОТ нагрузки В: а)в = у В1 -1= В

Ординаты эпюр единичной нагрузки: для умножения на со:

для умножения на oj: Прогиб в точке В

Отсюда

\ 2 3 Ь А j

B=ql.

Дальше решение идёт, как указано в § 137.

579�6703

§ 139] ВЫБОР ЛИШНЕЙ НЕИЗВЕСТНОЙ Н ОСНОВНОЙ СИСТЕМЫ

WTVl

§ 139. Выбор лишней неизвестной и основной системы.

В предыдущем примере мы выбрали за лишнюю неизвестную реакцию В. Мы могли бы выбрать и момент Жд. Соответствешо изменилась бы основная система и ход решения. Окончательный же результат, конечно, получился бы прежним.

Возьмём за лишнюю неизвестную опорный момент Ма (фиг. 363, а). Какой будет основная система? Чтобы получить её, надо отбросить то опорное закрепление, которое создаёт момент Жд, т. е. защемление конца Л. Чтобы на конце А не было опорного момента, там следует поставить шарнирно- i- неподвижную опору.

Основной системой будет балка, изображённая на фиг. 363, б. Загрузим её внешней нагрузкой и опорным моментом Жд (фиг. 363, в).

Чтобы балки фиг. 363, awe работали одинаково, надо для балки фиг. 363, в написать дополнительное условие, что сечение А под действием изображённых нагрузок не может поворачиваться; накладываем это ограничение на перемещение, соответствующее выбранной лишней неизвестной:

вд = 0.

Далее, применив для решения уравнения вд = О теорему Кастильяно, имеем

6)

Фпг. 363.

Mdx дМ

EJ дМ,

следовательно,

Mdx дМ

EJ дМ.

= 0.

Для нахождения М и -щ- выразим реакцию В основной системы (фиг. 363, в) через Жд и произведём все обычные вычисления:

2 дМ

х I

Отсюда

11 I

dx = 0;

6 8 3 -

т. е. той же величине, которая была получена раньше. Дальнейший ход решения не отличается от разобранного выше.

Решение той же основной системы (фиг. 363, в и 364, а) с при-

менением способа Вереш.агина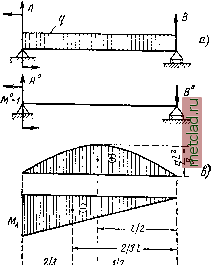

потребует изображения второго состояния загружения основной системы моментом = 1 (фиг. 364, б) и построения эпюр изгибающего момента: от заданной нагрузки q (фиг. 364, в), от момента Ма (фиг. 364, г) и от единичной нагрузки М = 1 (фиг. 364, д). Пользуясь формулой

9 (21.22), вычисляем бд:

-Ма~1

2 3

= 0.

Как видно, уравнение для определения Ма полностью 2) совпадает с найденным по Кастильяно.

Сравнивая два варианта решения поставленной задачи с лишней ф неизвестной Вис лишней неизвестной Ма, видим, что при применении способа Кастильяно первый вариант менее сложен по вычислениям. Это объясняется тем, что основной системой в первом варианте является балка, защемлённая одним концом, во втором же - балка на двух опорах; для второй - вычисления сложнее. Таким образом, лишнюю неизвестную и, следовательно, основную систему надо выбирать с таким расчётом, чтобы выкладки (вычисление изгибающих моментов и т. д.) были проще.

Фиг. 364.

Подставляя полученные данные в (23.7), находим;