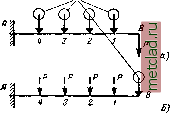Полная работа внешних сил составится из трёх частей; работы силы на вызванном ею прогибе у, т. е. у РгУпу работы силы Р

на вызванном ею прогибе её точки приложения у, т. е. - Рз*

наконец, работы силы Pj на прогибе её точки приложения от силы Рз, т. е. Piyic,

Таким образом, накопленная в стержне при действии обеих сил энергия будет равна:

РУп + у + РУ -

Это количество энергии деформации зависит лишь от конечных значений сил и прогибов и не зависит от порядка нагру-жения.

Если к балке, загружённой силой Р, приложить затем силу Р, то, повторив цепь вычислений, получим:

= у Р2УП + у РхУп + (21.18)

Сравнивая оба значения U, получаем:

Р1Уп = РУп. (21.19)

т. е. работа силы Pj (или первой группы сил) на перемеш,ениях, вызванных силой (второй группой сил), равна работе сил Р на перемещениях, вызванных силой Pi.

Это и есть теорема о взаимности работ. Её можно сформулировать и иначе: работа первой силы (Pi) при действии второй (Р)

ПрогиЗомерь. Р РО ВТОрОЙ СИДЫ при дей-

ствии первой.

Если взять частный случай, когда Рх = Pg, то получим теорему о взаимности перемещений: 12=21, т. е. прогиб точки 1, вызванный силой, приложенной в точке 2, равен прогибу точки 2, вызванному такой же силой, но приложенной в точке Л

Пользуясь этим свойством взаимности, можно, например, упростить производство Фиг. 337. опытов по определению деформаций.

Пусть мы хотим опытным путём найти прогибы в сечениях /, 2, 3, 4 балки, зашемлённой одним концом Л и нагружённой на другом (В) силой Р (фиг. 337). Вместо того чтобы ставить для каждой точки свой прогибомер (фиг. 337, а) или переносить прибор, что всегда очень неудобно и может повлечь ошибки, можно поступить иначе. Поставим прогибомер в точке В, а силу Р будем последовательно прикладывать в сечениях /, 2, 3, 4 (фиг. 337, б)\ измеренные в точке В прогибы и будут по теореме о взаимности перемещений равны прогибам точек 1, 2, 3, 4 от силы Р, приложенной в точке В.

приложения силы Pf, тогда

так как Р, Рз, ... , Afi, Ж2,... , q 2, ... 1 fli, flj, ... > *ь 2, ... , с?, ... при этом I дифференцировании постоянны. Но мож- но рассматривать как численную вели- /1# чину момента Ж в любом сечении бал-ки от действия так называемой единич-ной нагрузки, т. е. силы Pi = l; действительно, подставляя в формулу (21.20)

вместо Pi его частное значение, единицу, и приравнивая все остальные нагрузки нулю, получаем M = ai,

Например, для балки, изображённой на фиг. 338, а, изгибаюш.ий момент равен:

М{х) = - Рх - .

гт дМ(х)

Производная --ф = - х\ но это как раз и будет выражение изгибающего момента нашей балки, если мы её нагрузим силой /, приложенной в той же точке В, где расположена сила Р (фиг. 338, б), н направленной в ту же сторону.

Аналогично, производная изгибающего момента М{х) по паре сил Ml численно представляет собой изгибающий момент от пары С моментом, равным единице, приложенной в том же сечении где Имеется пара Afi, и направленной в ту же сторону. Таким образом, вычисление производных изгибающего момента можно заменить

§ 130. Теорема Максвелла - Мора.

Прогиб балки в точке приложения сосредоточенной силы Р равен:

У={; (21.15)

аналогичное выражение мы имеем и для угла поворота с заменой производили на Выясним, что представляют собой эти

производные.

Если на балке расположена какая угодно нагрузка из сосредоточенных сил Pi, Pj, Рз, ... , моментов Mi, М, ... , сплошных нагрузок 1, qj , у то момент М (х) в любом сечении такой балки выражается линейной функцией от нагрузок:

М{х) = а,Р, + а,Р,+ ... -b,M, + b,M,- ... +qi+ ... (21.20)

Коэффициенты ai, а.2, ... , i, 2 являются функциями

пролёта балки, расстояний точек приложения сил и моментов от опор и абсциссы X взятого сечения. Пусть мы отыскиваем прогиб точки

вычислением изгибающих моментов от единичной нагрузки. Эти моменты мы будем обозначать буквой Л4.

Таким образом, для отыскания перемещения В (прогиба или угла поворота) любого сечения балки, вне зависимости от того, приложена или не приложена в этом сечении соответствующая сила, необходимо найти выражение для изгибающего момента М от заданной нагрузки и момента от соответствующей единичной нагрузки,

приложенной в сечении, где ищем перемещение Ь\ тогда это перемещение выразится формулой

b={dx. (21.21)

♦ t

J

I f

Эта формула была пред-6) ложена Максвеллом в 1864 г. и введена в практику расчёта О. Мором в 1874 г. Если мы в формуле (21.21) / под 8 подразумеваем прогиб, Фиг. 339. то момент надо вычис-

лять от сосредоточенной единичной силы, приложенной в той точке, где мы отыскиваем прогиб; при вычислении же угла поворота в качестве единичной нагрузки прикладывается пара сил с моментом, равным единице. Для примера фиг. 338 имеем:

7И = -р. -2(фиг. 338, а),

Ж = - 1 Х = - х (фиг. 338, б).

Знак плюс означает, что направление перемещения совпадает с направлением единичной нагрузки, знак минус - наоборот.

Если при определении изгибающих моментов придётся делить балку на участки, то соответственно и интеграл в формуле распадётся на сумму интегралов.

Сравнивая формулу Кастильяно (21.15) и (21.16) с формулой Мора (21.21), нетрудно заметить, что они отличаются лишь одним

множителем. В теореме Кастильяно или , в теореме Мора Ж.

Следовательно, производная от изгибающего момента по обобщённой силе - это то же самое, что изгибающий момент от силы Р = 1.