В частном случае значение прогиба:

при а=Ь =

получаем хорошо известное уже

48ЕУ

Иногда, при малом количестве внешних активных сил, определение величины потенциальной энергии при изгибе можно производить, минуя формулу (21.8), путём вычисления работы внешних сил.

Рассмотрим, например, балку (фиг. 326), защемлённую концом Л. и нагружённую на конце В сосредоточенной силой Р. Пролёт балки /. На балку действует заданная сила Р и вызванные ею реакции Л, Мд и Яд. Так как опорное сечение неподвижно, то реакции работы при деформации балки не производят. Работу даёт лишь сила Р; прогиб конца балки при постепенном возрастании силы Р связан с ней линейной зависимостью:

ЪfEJ

работа сила Р

1 Р2/3 pEJ

2 6/ ~ 2/3

Если на элемент конструкции будет действовать несколько сил, то полная потенциальная энергия получится суммированием таких произведений, вычисленных при совместном действии на конструкцию всех этих сил, так как каждое перемещение будет зависеть от всей нагрузки.

Фиг. 326.

1 I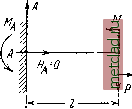

Фиг. 327.

Например, при действии на балку, защемлённую концом (фиг. 327), силы Р и пары М, приложенных на свободном конце В, потенциальная энергия будет равна:

р/з МП

2EJ РМП

+ уЛ1

РП \ 2EJI

6EJ 2EJ 2EJ В двух последних примерах для определения величины работы внешних сил Ар-и требовалось знать величину прогиба или угла поворота в сечении приложения внешней силы.

§ 126. Теорема Кастильяно.

Установим теперь метод определения перемещений, основанный на вычислении потенциальной энергии деформации. Поставим себе задачу нахождения перемещений точек упругой системы по направлению действия приложенных к этой системе внешних сил.

Будем решать эту задачу в несколько приёмов; сначала рассмотрим более простой случай (фиг. 328), когда на балку в сечениях /, 2, 5,... действуют только сосредоточенные силы Р, Р, Рз, ... и т. д. Под действием этих сил балка прогнётся по кривой / И останется в равновесии.

Прогибы сечений 1, 2, 3, в которых приложены силы Pj, Яз, Яз, обозначим y<iy у, ... и т. д. Найдём один из этих прогибов, например у - прогиб сечения, в котором приложена сила Pi.

Переведём балку, не нарушая равновесия, из положения / в смежное положение , показанное на фиг. 328 пунктиром. Это

можно сделать различными приёмами: \f добавить новую нагрузку, увеличить

/ 1 уже приложенные и т. д.

д.]-1-представим себе,. что для пе-

t;---! Z --fmj рехода к смежному деформированному

--Jy/- состоянию к силе Р сделана беско-

2. нечно малая добавка dP (фиг. 328);

чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.

При переходе от состояния / балки к состоянию И все нагрузки Р опустятся, значит, их потенциальная энергия уменьшится. Так как равновесие не нарушалось, то уменьшение энергии нагрузок dUp целиком преобразовалось в увеличение потенциальной энергии деформаций балки dU. Величина dUp измеряется работой внешних сил при переходе балки из положения / в положение Я:

dU=dAp, (21.10)

Изменение dU потенциальной энергии деформации, являющейся функцией сил Pi, Pj, Pg, ..., произошло за счёт очень малого приращения одной из этих независимых переменных Pf, поэтому дифференциал такой сложной функции равен:

dU=dP,. (21.11)

Что касается величины dAp, то эта работа в свою очередь является разностью работы нагрузок Р для положений U и 1:

dAp=A - А.

Работа Ах при одновременном и постепенном возрастании сил Р равна:

При вычислении работы Л2 учтём, что её величина всецело определяется окончательной формой деформированной балки (§ 125) и не зависит от порядка, в котором производилась нагрузка.

Предположим, что мы сначала нагрузили нашу балку грузом dP, балка очень немного прогнётся (фиг. 329, положение /), и прогибы её в точках /, 2, 3 будут dy\, Уъ 4Уз- Работа статически приложенной нагрузки dPi будет равна

dPidyi. После этого начнём постепенно нагружать балку одновременно возрастающими грузами Р, Р<, Рд.

К первоначальным прогибам dy, dy%y 4Уз добавятся прогибы yi, уу Уъ (фиг. 329). При этой стадии нагружения силы Pj, Р2, р3 произведут работу -i- Ру -f- у Ру у РъУъ=А\\

кроме этого, произведёт работу уже находившийся на балке груз flfP,; он пройдёт путь j/i, и так как при втором этапе нагружения он оставался постоянным, то его работа равна dPy, Балка займёт положение /7, показанное на фиг. 329 пунктиром.

Таким образом, полная работа, проделанная внешними нагрузками при переходе балки из недеформированного состояния в положение Пу будет равна (фиг. 329)

A, = -dP,dy,-\-A, + dP,y,.

Теперь вычислим

dU= dAp=A - Ai= dPdyi -f d P,y.

Пренебрегая слагаемым второго порядка малости, получаем:

dAp=dPyi, (21.12)

Подставляя полученные значения dU (21.11) и dAp (21.12) в уравнение (21.10), находим

Уг = §. (21.13)

Таким образом, в рассмотренном случае прогиб точки приложения сосредоточенной силы Р, равен частной производной потенциальной энергии деформации по этой силе.