ОТДЕЛ VI.

ДЕФОРМАЦИИ БАЛОК ПРИ ИЗГИБЕ.

ГЛАВА XVIIf.

АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ.

§ 108. Прогиб и поворот сечения балки.

При действии внешних сил, расположенных в одной из главных> плоскостей инерции балки, наблюдается искривление её оси в той же плоскости, происходит так называемый плоский изгиб.

На фиг. 278 изображена в искажённом масштабе искривлённая ось балки, защемлённой одним концом и нагружённой на другом конце сосредоточенной силой. Центр тяжести О какого-либо сечения с абсциссой X перемещается в точку Oi-

Перемещение OOi центра тяжести сечения по направлению, перпендикулярному к оси балки, называется прогибом балки в этом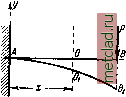

Фиг. 278.

Фиг. 279.

сечении или прогибом этого сечения балки. Прогиб будем обозначать буквой у.

Строго говоря, так как ось балки, лежащая в нейтральном слое, не меняет при изгибе своей длины, то точка Oi сместится несколько в сторону от перпендикуляра к оси балки. Однако обычно прогибы у малы по сравнению с длиной балки, и указанное смещение в сторону является величиной уже 2-го порядка малости по отношению к длине балки, - им поэтому пренебрегают.

При деформации балки сечение, оставаясь плоским, поворачивается по отношению к своему прежнему положению. На фиг. 279 изображено сечение 7 до и после деформации. Угол 0, на который каждое сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения. Для практических целей необходимо уметь вычислять прогибы и повороты для любого сечения балки.

Величина наибольшего прогиба может служить мерилом того, насколько искажается форма конструкции при действии внешних сил. Обычно с целью сохранения соединений частей балки от расшатывания и уменьшения колебаний под действием подвижной нагрузки ограничивают величину наибольшего прогиба балки под нагрузкой. Так, для стальных балок в зависимости от назначения их ставят

условием, чтобы прогиб не превосходил -уо 250 пролета.

Кроме того, знание деформаций балки нам потребуется при решении статически неопределимых задач, когда число опорных реакций превышает число уравнений статики. Дополнительные уравнения могут быть написаны лишь путём изучения деформаций конструкции. Для того чтобы полностью знать деформацию балки, необходимо уметь вычислить для каждого сечения его прогиб у и угол поворота б. Оба они будут функциями от х - расстояния сечения от начала координат; между у и В для каждого сечения имеется определённая зависимость.

Выберем систему координат, которой будем в дальнейшем пользоваться. Начало координат расположим в одной из точек первоначальной оси балки, которую всегда будем выбирать за ось х\ ось у будем направлять перпендикулярно первоначальной оси балки вверх. При таких условиях уравнение

у=/\х) (18.1)

представит собой уравнение кривой, по которой изогнётся ось балки под нагрузкой; это будет уравнение изогнутой оси балки.

Касательная к изогнутой оси балки (фиг. 279) в точке Oi составит с осью X угол; равный б, т. е. углу поворота поперечного сечения относительно первоначального положения. С другой стороны, тангенс угла, образованного касательной к кривой >=/(дг) с осью х, как известно, равен

tg6 = -g.. (18.2)

Так как на практике прогибы балки обычно малы по сравнению с пролётом, то б бывают очень малыми углами, обычно не больше 1°. Для таких углов можно считать, что тангенс угла равен углу, выраженному в радианах. Отсюда следует, что

6 = . (18.3)

Т. е. угол поворота сечения равен первой производной по х от прогиба у в этом сечении.

Таким образом, задача изучения деформации балки сводится к получению уравнения изогнутой оси y=f(x)\ зная его, мы можем вычислить дифференцированием и угол поворота для любого сечения балки.

§ 109]

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ

§ 109. Дифференциальное уравнение изогнутой оси.

Для того чтобы получить у как функцию от х, надо установить зависимость деформации балки от внешних сил, изгибающих её, от ее разме м материала. Такая зависимость была нами получена уже раньше в § 78.

Используем формулу (13.10), полученную нами при рассмотрении чистого изгиба. Распространяя её на общий случай изгиба, то есть пренебрегая влиянием поперечной силы на деформации балки, можем написать

1 М{х) р(х) - EJ

где р (лг) - радиус кривизны участка изогнутой оси балки между двумя смежными сечениями на расстоянии х от начала координат; М(х) - изгибающий момент в том же сечении; EJ-жёсткость балки. Влияние Q{x) на деформации балки обычно невелико; метод его учёта дан в § 132.

На фиг.. 280 изображено изменение радиусов кривизны по мере изменения изгибающего момента. Для получения уравнения изогнутой оси необходимо использовать математическую зависимость между радиусом кривизны оси и координатами её точек х и у:

dy \2 3*

\dlc

(18.4)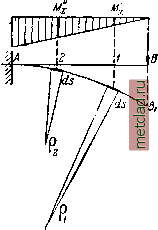

Фиг. 280.

Подставляя это значение для кривизны

в формулу (13.10), получаем дифференциальное уравнение, связывающее у, лг, М{х) и EJ:

dx М(х)

EJ

(18.5)

Это - так называемое дифференциальное уравнение изогнутой оси, или, как его часто называют, дифференциальное уравнение упругой линии .

Для громадного большинства практически встречающихся задач величина, представляющая собой угол поворота сечения балки.