Радиальные базисные функции описаны Бишопом (Bishop, 1995, стр. 164). Развернутое описание радиальных функций и их связей со сплайнами и методами кригинга можно найти в работах Ciessie (1993, стр. 180) и Chiles и Delfiner (1999, стр. 272).

Геометрическая анизотропия

Геометрическая анизотропия учитывается как преобразование координат:

4 0 0

где в - угол поворота и r - соотношение размеров малой и большой оси результирующего эллипса. Расстояние затем рас-

считывается как s

Диалог Declustering (Декластеризация) Декластеризация по ячейкам

По разным причинам данные могли быть отобраны неравномерно, с различной густотой опорных точек для разных участков территории. Для некотор1х методов преобразований, таких, как преобразования по методу нормальных меток, важно, чтобы гистограмма выборки правильно отражала гистограмму всей совокупности. Решением для неравномерных выборок является присвоение данным весовых значений, при этом данным, отобранным на территориях с высокой густотой точек, присваиваются меньшие веса. За более детальной информацией обратитесь к книгам Journel (1983), Isaaks и Srivastava (1989, стр. 421), Cressie (1993, стр. 352), и Goovaerts (1998, стр. 76).

Метод по умолчанию-Индекс Морисита (Morisitas index)

По умолчанию в модуле Geostatistical Analyst используется метод грида с квадратными ячейками, размер которых определяется исходя из максимального значения индекса Морисита (Morisitas index) (Morisita, 1959; см. также Cressie, 1993, стр. 590), где индекс Морисита - функция размера ячейки.

Полигональный метод

Возможно также использовать метод, который позволяет присваивать весовые значения в зависимости от размера полигонов, окружающих каждую точку. Полигоны образуются путем нахождения всех возможных точек, которые ближе к данной опорной точке, чем к любой другой опорной точке. Таким образом, каждая опорная точка имеет полигон влияния. В математике такие полигоны носят название диаграмм Вороного и полигонов Тис-сена. За разъяснениями обратитесь к работам Isaaks и Srivastava (1989, стр. 238), и Goovaerts (1998, стр. 79). В модуле Geostatistical Analyst внешняя граница несколько больше, чем наименьший (без поворота) прямоугольник, который охватывает все точки. Прямоугольник образуется путем суммирования наибольшей х-координаты и у-координаты и 1/ 2 * VsTN , где S - площадь прямоугольника, а N - число наборов данных. Самые маленькие значения координат x и y несколько уменьшаются аналогичным

образом. Внешняя граница оказывает значительное влияние на весовые коэффициенты краев1х точек.

Диалог моделирования распределения

Преобразование по методу нормальных меток

Для некоторых методов кригинга важно, чтобы данные подчинялись закону нормального распределения. Один из способов привести распределение данных к нормальному - использовать преобразование по методу нормальных меток. За разъяснениями обратитесь к книгам Journel and Huijbregts (1978, стр. 478), Isaaks и Srivastava (1989, стр. 469), Cressie (1993, стр. 281), Rivoirard (1994, стр. 46), Goovaerts (1998, стр. 266), и Chiles and Delfiner (1999, стр. 380). Однако многие иллюстрации в этих источниках вводят в заблуждение, поскольку на них показано, что функция кумулятивного распределения необработанных данных является непрерывной. В действительности это ступенчатая функция. Пусть статистический ряд данн1х выглядит следующим образом: Z(s(1)), Z(s(2)), Z(s(n)), где Z(s(1)) - самое низкое значение, а Z(s(n)) - самое высокое значение. Предположим, что у нас есть только четыре значения (n = 4); тогда эмпирическая функция кумулятивного распределения будет выглядеть примерно следующим образом:

Кумулятивная вероятность

3/4 1/2

1/4 -I

Z(s(1))

Z(s(2)) Z(s(3)) Значение

Z(s(4))

Эта функция может быть сглажена различными способами. Также обратите внимание, что весовые значения по оси у - не должны быть приращениями (1/n;, если используется декластериза-ция по методу ячеек. Для выполнения преобразований в модуле Geostatistical Analyst предусмотрено несколько методов.

Прямой способ

Смешанный Гауссов метод

Он использует значения, которые соответствуют половине шага графика функции эмпирического распределения. На рисунке показано соответствие между исходными и трансформированными данными.

Эмпирическое кумулятивное распределение

Преобразование по методу нормальных меток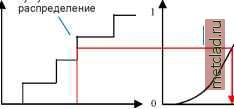

Кумулятивное распределение для стандартного нормального распределения -►

-3 0 3

Нормальное распределение

Z(S(1)) Z(S(2)) Z(S(3)) Z(S(4))

Исходные данные

Линейный метод

Линейный метод выполняет линейную интерполяцию по частям для исходной функции кумулятивного распределения. Суть этого метода легко понять, изучив рисунок:

Смесь из Гауссовых распределений может быть использована для сглаживания функции плотности вероятности. Модель функции плотности вероятности выглядит следующим образом:

p(z) = Pi(z;,aj)

exp

(z -a)2

Параметры a, и a. оцениваются по степени максимального сходства, предполагая смесь из нормальных распределений и независимых данных. Кумулятивное распределение вгчисляет-ся через числовое интегрирование,

Кусочные линейные интерполяции эмпирического кумулятивного распределения

Преобразование по методу нормальных меток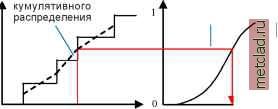

Кумулятивное распределение для стандартного нормального распределения -►

Z(S(1)) Z(S(2)) Z(S(3)) Z(S(4))

Исходные данные

-3 0 3

Нормальное распределение

P(z) = I p(x)dx

и между P(z) и кумулятивным распределением для стандартного нормального распределения устанавливается соответствие, аналогично тому, как это делается при прямом и линейном методах.