Использование преобразований по методу нормальных меток

По методу нормальных меток данные будут преобразованы и приведены к одномерному нормальному распределению, что позволит применить к ним методы простого и дизъюнктивного кригинга.

Желательно сравнить подобранную модель с эмпирической функцией кумулятивного распределения для каждого из трех методов аппроксимации, используемых в преобразованиях по методу нормальных меток.

Моделирование распределений

1. Для исследования распределения выберите интерполяцию по методу простого или дизъюнктивного кригинга.

2. В диалоге Выбор геостатистического метода, из меню Преобразование выберите опцию По методу нормальных меток.

Нажмите Далее.

3. 4.

Или, чтобы поменять способ отображения графика, выберите опцию Кумулятивное распределение.

Или, задайте количество столбцов, которое должно быть отображено на гистограмме.

В окне Выбор набора данных выберите другой набор данных (только для кокригинга, когда у вас есть два или большее количество наборов данных).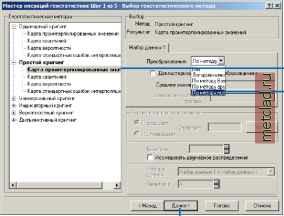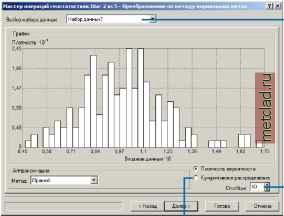

Проверка на двумерное нормальное распределение

Дизъюнктивн1й кригинг требует соблюдения условия подчинения даннгх двумерному нормальному распределению. Помимо этого, для того, чтобы создать картах вероятности и квантилей, предположим, что данн1е подчиняются полному многомерному нормальному распределению. Чтобы проверить данные на одномерное нормальное распределение, вы можете воспользоваться нормальнхми графиками КК. Теперь проверим данные на двумерное нормальное распределение. (Ни одна из этих проверок не гарантирует, что данн1е подчиняются полному многомерному нормальному распределению, но иногда разумно выдвинуть это предположение, основываясь на использовании этих инструментов диагностики.) Рассмотрим следующее вероятностное утверждение:

f(p,h) = Prob[Z(s) < Zp, Z(s + h) < Zp]

где zp - стандартный нормальнхй квантиль для некоей вероятнос-тир. Например, известно! значения стандартн1х нормальн1х квантилей: при р = 0.975, zp = 1.96; при р = 0.5, zp = 0; а при р = 0.025, zp = -1.96. В1ражение вероятности, приведенное в1ше, берет значение переменной Z в точке s и другой переменной Z в некоей точке s + h, и дает значение вероятности того, что оба этих значения меньше zp. Эта формула вероятности является функцией f(p,h), зависящей от р (и, соответственно, zp) и h. Функция будет также зависеть от степени автокорреляции между Z(s) и Z(s + h).

Теперь предположим, что Z(s) и Z(s + h) подчиняются двумерному нормальному распределению. Если значение автокорреляции известно, для функцииf(p,h) существуют формулы. Предположим, что h - константа, и только значение р меняется. Тогда можно предположить, что функция будет вхглядеть следующим образом: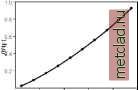

Правый график похож на график кумулятивного распределения вероятности. Теперь предположим, что значение р остается постоянным, и функция f(p,h) меняется в зависимости от h.

Предположим, что значение h очень мало. В этом случае, вероятность Prob [Z(s) < zp, Z(s + h) < zp] очень близка к вероятности Prob [Z(s) < zp] = р. Далее, предположим, что значение h очень велико. В этом случае, вероятность Prob[Z(s) < z , Z(s + h) < z ] очень близка к вероятности Prob[Z(s) <zp]fProb[Z(s + h) < zp] = р2 (потому что значения Z (s) и Z (s + h) практически независимы). Таким образом, для фиксированного значения р, следует ожидать, что значения функции f( р, h) будут меняться от р до р2. Теперь рассмотрим выражение f( р, h) как функцию обоих параметров р и расстояния h, вы можете наблюдать нечто похожее на следующем рисунке.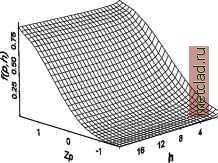

-15 -10 -0 5

Эта функция может бпть конвертирована в вариограммы и ковариационные функции для индикаторов. Если вероятность Prob[Z(s) < Zp, Z(s + h) < Zp] = E[I(Z(s) < Zp)fI(Z(s + h) < Zp)], где \(утверждение) - индикаторная функция, которая равна 1, если утверждение истинно, или 0, если утверждение ложно, тогда ковариационная функция для индикаторов с фиксированным значением р выглядит следующим образом:

CI(h;p) = f(p,h) - р2

а вариограмма для индикаторов с фиксированным р:

gI(h;p) = р - f(p,h)

Следовательно, вы можете оценить вариограмму и ковариационную функцию индикаторов исходных данных и использовать эту оценку для получения ожидаемгх вариограмм и ковариационнгх функций индикаторов для различнгх значений p. Например, они могут выглядеть следующим образом: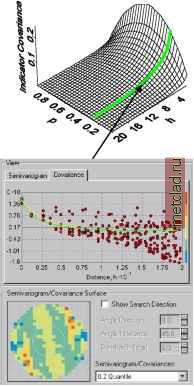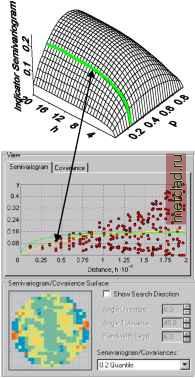

Красные точки на верхнем рисунке (в диалоге Моделирование вариограммы/ковариации) - это значения эмпирической ковариации и вариограммы для индикаторнхх переменных. Зеленая линия - это кривая, построенная теоретическим способом, для индикаторной вариограммы или индикаторной ковариации, предполагающая, что используемые данные подчиняются двумерному нормальному распределению, а желтая линия - модель, подобранная для исходных индикаторных даннхх. Таким образом, зеленая линия и желтая линия должны совпасть, если данные имеют двумерное нормальное распределение.