
 |
|
|
Главная --> Промиздат --> Интерполирование поверхности нения кригинга. Путем минимизации ожидания, в среднем, интерполятор кригинга близок насколько это возможно, к неизвестному значению. Решение для минимизации, ограниченное условием несмещенности, дает уравнения кригинга,
Эти уравнения станут более понятными, когда в следующем разделе вы подставите значения в матрицы. Помните, что цель состоит в решении уравнений для всех l, (весов), поэтому интерполятор может бпть образован с использованием S,l,Z (s,). Большинство элементов могут бпть подставлены, если вам известна вариограмма. В нескольких последующих разделах вы узнаете, как рассчитать значения вариограммы. Гамма-матрица G содержит смоделированные значения вариограммы для всех пар опорнгх точек, где означает смоделированные значения вариограммы, основанные на расстоянии между двумя опорными точками, определенными как точки г-ая и j-ая. Вектор g содержит смоделированные значения вариограммы для каждой пары из опорной точки и искомой точкой, где g,0 обозначает смоделированные значения вариограммы, основанные на расстоянии между г-ой точкой и искомой точкой. Также оценивается неизвестное значение m в векторе l; оно растет из-за условия несмещенности. Расчет эмпирической вариограммы Для расчета значений матрицы G мы должны изучить структуру данных путем создания эмпирической вариограммы. На варио-грамме показаны значения половины квадрата разности для пар точек (откладывается по оси y) в зависимости от расстояния между ними (откладывается по оси x). Первый шаг в создании эмпирической вариограммы - впчисле-ние расстояния и квадрата разности между значениями для каждой пары точек. Расстояние между двумя точками рассчитывается с использованием Эвклидова расстояния: Xj )2 + (У г Эмпирическая дисперсия - это половина квадрата разности 0.5 * среднее [(значение в точке г - значение в точке ,/ )2 ].
Как видите, для больших наборов данных (с большим количеством измеренных опорных точек) число пар точек будет быстро расти и станет неуправляемым. Следовательно, вы можете сгруппировать пары точек; такой процесс известен как бининг. В данном примере, бин - это заданный диапазон расстояний. Это означает, что все точки, находящие на расстоянии от 0 до 1 сгруппи- рованы в первый бпп, те точки, которые паходятся на расстоянии от 1 до -2 метров друг от друга сгруппированы во второй бпп, п т.д. Берется средняя эмпирическая дисперсия для всех пар точек. В нашем примере, данные распределены в пять бинов.
Подбор модели Теперь вы можете отобразить на графике - эмпирической вари-ограмме - среднюю дисперсию в зависимости от среднего расстояния для бина. Но значения эмпирической вариограммы не могут бпть использованы непосредственно в матрице G, поскольку вы можете получить отрицательные стандартные ошибки вычислений; вместо этого вы должны подобрать модель для эмпирической вариограммы. После подбора модели, вы будете использовать полученную модель для определения значений вари-ограммы для различных расстояний. 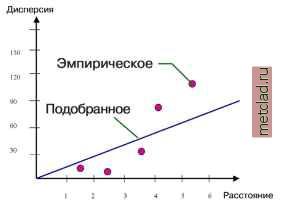 Для простоты, подобранная вами модель - линия регрессии, построения с использованием метода наименьших квадратов, имеющая положительный угловой коэффициент и проходящая через ноль. В модуль Geostatistical Analyst включено большее количество моделей, которые можно использовать для подбора. Формула для определения дисперсии для любого заданного расстояния в нашем примере выглядит следующим образом: Дисперсия = Угловой коэффициент * Расстояние Угловой коэффициент определяет наклон подобранной прямой. Расстояние - это расстояние между парами точек, оно обозначается как h. В нашем примере, дисперсия для любого расстояния может быть определена по формуле: Дисперсия = 13.5*h Теперь создадим матрицу значений G. Например, значение g2 для точек (1,5) и (3,4) в уравнении равно: Дисперсия = 13.5 * 2.236 = 30.19
В приведенном выше примере, для пары точек (1,5) и (3,4), величина лага была вычислена с использованием расстояния между двумя точками (см. предыдущую таблицу). Значение варио-граммы определяется путем умножения углового коэффициента, равного 13.5, на расстояние. Единицы и нули в нижней строке и крайнем правом столбце определены в соответствии с условием несмещенности. Формула значений матрицы для ординарного кригинга следующая: G*l = g Теперь, когда построена матрица G, необходимо найти значения вектора 1, содержащего значения весов, которые будут присвоены измеренным значениям, находящимся вокруг искомой точки. Поэтому, выполним простую операцию из матричной алгебры и получим следующую формулу: 1 = G-1 * g где G1 - обратная матрица G. Обратную матрицу G получаем, выполнив операцию линейной алгебры.
Далее, для искомой точки строится вектор g. Например, рассмотрим точку (1,4). Вгчисляем расстояние от точки (1,4) до каждой из точек с измереннгми значениями (1,5), (3,4), (1,3), (4,5), и (5,1). Исходя из этих расстояний, определяем подобранную дисперсию по формуле Дисперсия = 13.5* h, выведенной ранее. Вектор g для точки (1,4) приведен в следующей таблице. Точка Расстояние g Вектор для (1,4) (1,5)
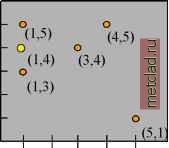 1 2 3 4 5 X Теперь, после того, как были созданы матрица G и вектор g, вгчислим вектор весов кригинга: 1 = G-1 * g. Для этого, воспользуемся линейной алгеброй. Веса приведены ниже в таблице. Выполнение интерполяции Теперь, когда у вас есть значения весов, умножьте вес каждого измеренного значения на это значение. Сложите результаты и получите искомое значение для точки (1,4).
Далее, изучите полученный результат. На следующем рисунке показаны веса (в скобках) точек с измеренными значениями, использованными для нахождения значений в искомой точке (1,4).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||