Но что если вы захотите описать плоскость, которая соответствовала бы долине? Получить достоверную поверхность, использовав для ее описания плоскость, было бы довольно сложно. Однако, если у вас только один перегиб плоскости (см. нижний рисунок), вы сможете подобрать более точную поверхность, чем плоскость (то есть, получить более близкие значения для большего количества значений). Возможность описания одного перегиба поверхности - основа интерполяции по методу глобального полинома второго порядка. Два перегиба плоскости могут бпть описан! полиномом третьего порядка, и так далее. Перегибы могут бпть расположены в двух направлениях, и тогда можно будет описать поверхность в форме чаши .

Визуализация интерполяции по методу локальных полиномов

Теперь рассмотрим, что происходит, когда поверхность сначала является наклонной, затем выравнивается, а затем снова образует склон. Попптка описать этот участок плоскостью даст плохие результаты. Однако, если вы сможете использовать несколько меньших перекрывающих плоскостей, а затем использовать центр каждой плоскости как интерполируемое значение для каждой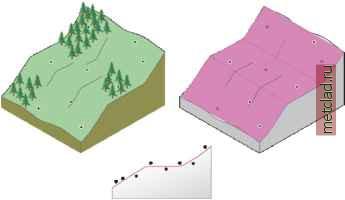

точки на этой плоскости, результирующая поверхность будет более гибкой и возможно более точной. Это концептуальная основа для интерполяции по методу локальных полиномов.

Визуализация радиальных базисных функций

Радиальн1е базиснхе функции позволяют строить поверхности, учит1вающие глобальнхй тренд наряду с локальнхми вариациями. помогает в тех случаях, когда подбор плоскости для значений в опорнхх точках не дает точного описания поверхности.

Чтобы построить поверхность, допустим, что у вас есть возможность изогнуть и растянуть интерполируемую поверхность таким образом, чтобы она прошла через все опорные точки. Существует много способов для определения формы поверхности в промежутках между опорными точками. Например, вы можете заставить поверхность образовывать изящные изгибы (плоский сплайн), или вы можете контролировать, насколько крепко вы тяните за края поверхности (сплайн с натяжением). Это концептуальная основа интерполяции, основанная на радиальных базисных функциях.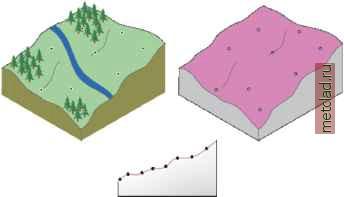

Что такое геостатистические методы

Геостатистические решения

Итак, способы, рассмотренные нами, относятся к детерминистским методам интерполяции, поскольку они напрямую основаны на измеренных значениях опорных точек в окрестностях искомой или на заданных математических формулах, которые определяют сглаживание результирующей поверхности. Второе семейство методов интерполяции состоит из геостатистических методов, которые основаны на статистических моделях, учитывающих автокорреляцию (статистические взаимоотношения между опорными точками). С помощью этих методов можно не только построить искомую поверхность, но и получить некую количественную оценку точности интерполяции.

Далее вы рассмотрите основные шаги применения методов геостатистики на примере ординарного кригинга.

Кригинг аналогичен методу взвешенных расстояний (IDW) в том, что опорным точкам из окрестности искомой точки, для получения ее значений, присваиваются веса. Однако веса основаны не только на расстоянии между измеренными точками и искомой точкой, но и на распределении опорных точек в пространстве в целом. Чтобы учесть расположение в пространстве, придав точкам весовые коэффициенты, необходимо количественно определить пространственную автокорреляцию.

Чтобы решить задачу геостатистического анализа, необходимо пройти несколько этапов.

Расчет эмпирической вариограммы-кригинг, как и большинство способов интерполяции, построен на предположении, что объект!, расположенные поблизости, более похожи друг на друга, чем удаленные друг от друга объекты (это предположение в данном примере количественно определенно как пространственная автокорреляция). Эмпирическая вариограмма - это средство для исследования связей между точками. Пары, расположенные на близком расстоянии, должны иметь меньшую разницу в измеренных значениях, чем те опорные точки, которые

удалены друг от друга. То, насколько это предположение верно, может быть изучено по эмпирической вариограмме.

Подбор модели-осуществляется путем подбора линии, которая наилучшим образом проходит через точки на графике эмпирической вариограммы. То есть, вы должны определить линию таким образом, чтобы (взвешенный) квадрат разницы между каждой точкой и линией был как можно меньше. Такой способ носит название подбора по методу (взвешенных) наименьших квадратов. Эта линия и будет моделью, количественно определяющей пространственную автокорреляцию в ваших даннгх.

Создание матриц-уравнения для ординарного кригинга содержатся в матрицах и векторах, которые зависят от пространственной автокорреляции между опорными и искомыми точками. Значения автокорреляции могут быть получены из модели ва-риограммы, описанной выше. Матрицы и векторы определяют веса кригинга, присваиваемые каждому измеренному значению.

Выполнение интерполяции-на основе весов кригинга, вы можете вычислить предполагаемое значение в искомой точке с неизвестным значением.

Проработка проблемы

Представьте, что вы на местности измерили значения высоты в пяти точках исследуемого вами ландшафта. Эти опорные точки показаны на нижнем рисунке оранжевым цветом. Рядом с каждой точкой даны ее координаты (X,Y).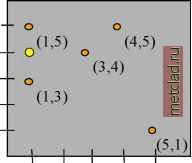

1 2 3 4 5

Значения высот:

в точке (1,5) высота =

в точке (3,4) высота =

в точке (1,3) высота =

в точке (4,5) высота = X 100

в точке (5,1) высота =

Уравнения кригинга

Для интерполяции значения в точке с координатами (1,4) (X= 1 и Y = 4), называемой искомая точка (желтая точка на рисунке), вы воспользуетесь методом ординарного кригинга. Модель ординарного кригинга определяется формулой

Z(s) = m + e(s)

где s =(X, Y) - положение точки; например, координаты одной из опорнгх точек s = (1,5), и Z(s) - значение измеренной величины для данной точки; например, для данной точки -Z(1,5) = 100. Модель основана на постоянном среднем m для данных (нет тренда) и случайных ошибках e( s) с пространственной зависимостью. Предположим, что случайнхй процесс e(s) является внутренне стационарным. Эти допущения обсуждаются в следующих разделах. Интерполятор может бпть получен

как взвешенная сумма данных,

Z(s ) - измеренное значение в г-ой точке, например, Z(1,5) = 100;

l, - неизвестный вес для измеренного значения в г-ой точке; s0 - координаты искомой точки, например, (1,4); и N = 5 - число опорнхх точек.

Формула аналогична формуле интерполяции по методу взве-шеннгх расстояний (IDW). Однако, в методе IDW, вес l зависит исключительно от расстояния до искомой точки. В ординарном кригинге, вес l зависит от вариограммы, то есть от расстояния до искомой точки, и от пространственных взаимосвязей между опорными точками, расположенными вокруг искомой точки.

При выполнении интерполяции для нескольких точек, некоторые из искомых значений окажутся выше или ниже фактических значений величин. В среднем, разность между проинтерпо-лированными значениями и фактическими значениями должна быть равна нулю. Такое условие называется условием несмещенности интерполятора . Для гарантии того, что интерполятор является несмещенным для неизвестного измерения, сумма весов l, должна бпть равна единице. Воспользовавшись этим ограничением, убедитесь, что разница между истинным значением, Z(s0), и интерполятором, Sl,Z(s,), имеет наименьшее из возможных значений. Это минимизирует статистическое ожидание следующей формулы, на основе которой получаются урав-

(So)-fAZ (Si)