Это будет так называемая третья внешняя краевая задача теории потенциала.

Полное решение этой задачи для поверхности Земли, данное Молоден-<кжм [36], достаточно сложно. Укажем лишь общий путь ее решения и приближенный результат, достаточный для последующих рассуждений и выводов.

Поскольку возмущающий потенциал Т обладает всеми свойствами потенциала притяжения, то его можно представить в виде потенциала притяжения некоторого фиктивного материального слоя плотности ф, распределенного на земной поверхности S (рис. 116). Элементарная масса, приходящаяся на элемент поверхности dS, будет (pdS. В точке А вне S эта масса создает элементарный потенциал

(62.16)

потенциал Т от всей массы слоя выразится

Ф dS

(62.17)

где г - расстояние от исследуемой точки до элемента поверхности dS.

Представленный в таком виде возмущающий потенциал будет вне масс гармонической и регулярной на бесконечности функцией, т. е. он удовлетворит условиям = О и Иш Г = 0. Но, определив по (62.17) возмущающий

г-*-со

потенциал, мы ввели неизвестную вспомогательную функцию ф. Таким образом, теперь вместо Т необходимо определять ф.

5 / / / М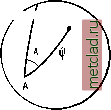

Рис. 117

Для этой цели воспользуемся условием (62.15), которому должен подчиняться возмущающий потенциал Т на поверхности S. Подставляя (62.17) в (62.15), получаем

>м

Ф dS

(62.18)

где Н - направление вертикали на Земле.

В качестве поверхности S в последнем выражении принимается близкая поверхность .S, для которой высоты точек равны Ну, точно получаемые из измерений (из нивелирования). Измеренные на всей поверхности Земли аномалии {gM - Ум) также можем считать отнесенными к этой поверхности Si-Поэтому в уравнении (62.18), если S заменить через S-, остается одно неиз-

вестное - плотность слоя ср. Не приводя подробностей дифференцирования ((62.18) и опуская сложные преобразования, напишем окончательный результат

2.<pcos( . H, = te-v)+ l + ilK (62.19)

St Si

тде {n, Н) - угол между нормалями к поверхности .sj и эллипсоиду;

- яо) - разность нормальных высот точек поверхности S.

Это основное интегральное уравнение, решающее задачу определения плотности ф введенного фиктивного слоя.

Полученное уравнение (62.19) для равнинных районов может быть упрощено. В этих районах можно положить Н - Hi = О при г -> 0; влияние отдаленных горных районов, где [Н - Hq) достигают значительной величины, будет также мало вследствие того, что это влияние определится выражениями

---- при большом значении] знаменателей. Следовательно, для равнинных

районов второй интеграл в уравнении (62.19) может не приниматься во внимание; можно также принять cos (тг. Я) = 1.

Но если принять Ю - Но = О, то поверхность Sj обратится в сферу радиуса R. Обозначая эту сферу через о, получаем

2яф = (-т)-г2-1. (62.20)

Решая интегральное уравнение (62.20), получаем выражение для ф. После тЕОДСтановки его в (62.17), т. е.

найдем решение этой задачи, данное Стоксом,

Ta=-jAgS{)dG, (62.21)

тде do - элемент поверхности сферы о;

ij) - сферическое расстояние от данной точки А до текущей точки М элемента do (рис. 117); (Ф) - функция Стокса, определяемая выражением

S {) = cosec -- - 6 sin -f-1 - 5 cos я)) - 3 cos фЬ (sin -f- sin --); (62.22)

R - радиус сферы о, т. е. радиус земного шара, который следует положить равным среднему радиусу Земли

R=y ab.

Элемент поверхности do можно выразить так:

do = i?2 sin ddA. (62.23)

Тогда выражение (62.21) для Т примет вид

я 2Я

Т=- AgS(t)sinddA. (62.24)

Зная Г, легко находим выражение для аномалии высоты. Действительно, так как, согласно (62.14),

я 2Я

S - j j Ag5 W sin t # dA. (62.26)

Как показали исследования, ошибка в , вызванная заменой поверхности Земли Si сферой а в равнинных районах, - величина третьего порядка малости, т. е. пренебрегаемая величина.

Для вычисления возмуш,ающего потенциала Г и на его основе величин , i ИТ) для горных районов необходимо исходить из полной формулы (62.19). Более точная, чем (62.24), и в то же время сравнительно простая формула для Г, учитывающая рельеф Земли, полученная на основе (62.19), может быть написана так:

л 2Я

T = \{Ag-\-6g)S (115) sin yddA, (62.27)

где bg приближенно равно [7, стр. 100, формулы (V.44)]

egsAgldo. (62.28)

Выражение (62.27) - упрощенная формула Молоденского первого приближения.