Тогда, учитывая соотношения (56.17) и (56.28) и интегрируя в пределах от Rl до R, получаем для потенциала слоя

y=4n/AJ RdR=~nfj{R-Rl). (56.29)

Введем в последнее выражение массу слоя. Масса слоя м выразится как произведение его объема на плотность

M = jn{R-R)6. (56.30)

Тогда для потенциала слоя получим

y-f~- (56.31)

Потенциал шара получится, если в (56.29) положить = тогда

у 4 л/ - (56.32)

или, принимая во внимание, что масса шара равна

M = nR4, (56.33)

приходим к формуле (56.31).

Сила притяжения выразится формулой

(56.34)

Итак, шар, состоящий из концентрических однородных слоев, притяги вает так, как будто вся его масса сосредоточена в центре. Иначе говоря, шар создает во внешнем пространстве потенциал, равный потенциалу точки с массой М, расположенной в его центре.

Теперь допустим, что притягивающая точка А расположена внутри шара на расстоянии р от центра О (рис. 110). Проведем через А концентрическую сферу, которая разделит массу на две части: массу слоя Sq, имеющего потенциал Vq, и массу шара Si, имеющего потенциал У. Очевидно, слой s, по отношению к которому точка А является внутренней, не притягивает точку.

На основании (56.18) и (56.13) получим

Fo - 4л:/б j Д - 2я/б (Л - р2). (56.35)

Согласно (56.29),

Потенциал слоя получится

F - Fo + Fi = 4 =/б ЗЯ2- р2 2 j . (56.36)

Для шара = О и тогда

F = jt/6(3/?2-p2). (56.37)

Дифференцируя (56.37) по р, получаем силу притяжения F

==-Т /6р- (56.38)

Масса т шара, ограниченного сферической поверхностью радиуса р, равна

иг -у лбр.

Поэтому выражение для силы притяжения F (56.38) примет вид

F==-f,

(56.39)

Следовательно, на основании (56.39) можно сделать вывод, что и в случае Бнутренней точки притяжение действует по закону Ньютона, т. е. обратно пропорционально квадрату расстояния и прямо пропорционально притягивающей массе с той только оговоркой, что в данном случае притягивает не вся масса шара, а только та, которая расположена внутри сферической поверхности, проходящей через точку. Точка А притягивается при этом так, как если бы вся масса внутреннего слоя (радиуса р) была сосредоточена в центре шара.

Из (56.38) очевидно, что притяжение массы всего шара действует по другому закону, т. е. прямо пропорционально расстоянию р от точки А до центра 0\ в центре шара р = О и, следовательно, сила притяжения также равна нулю.

Получим выражения для потенциала притяжения V и силы притяжения для случая, когда притягиваемая точка расположена на поверхности шара. Очевидно, в этом случае в соответствующих формулах равным R.

Делая указанную подстановку в формулы для потенциала (56.32) и <56.37) и в формулы для силы притяжения (56.34) и (56.38), получаем одинаковый результат, т. е.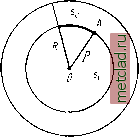

Рис. 110

следует положить р

Отсюда можно сделать вывод, что потенциал силы притяжения и его первая производная (составляющая силы притяжения) при пересечении границы тела однозначны и меняются непрерывно, без разрыва.

Вычислим вторые производные от потенциала для точки на поверхности шара, используя его выражения, полученные для положения точки вне и внутри шара.

Из (56.34) имеем

dW d dV (ip2 dp dp

dp Я

4 rc 8 B

(56.41) 247

или, при р - /?,

Из (56.38) получаем

dW d dV

dW 8 ,c = я/б.

(56.42)

(56.43)

Таким образом, значения вторых производных от потенциала при выходе притягиваемой точки на поверхность шара из внешнего пространства и изнутри различаются на величину 4л/б.

Э о значит, что вторая производная от потенциала, взятая по направлению нормали, при прохождении через поверхность шара имеет разрыв и изменяется скачком на величину 4л/б. Исследования показали, что и в более обпем случае, когда на поверхности, разделяющей две среды, плотность б меняется скачком, вторые производные потенциала также испытывают скачок. Это свойство вторых производных от потенциала имеет важное принципиальное значение.

§ 57. Уравнения Лапласа и Пуассона

Напишем потенциал силы притяжения

F = /j-. (57 1)

Образуем вторые производные по координатам

dW dW dW

Дифференцируя выражение (53.13)

дх J } г

получаем

дх \ дх ) J L

{а - х) дг

Так как

то находим окончательно

Аналогично

<9ж2

dW dy-dW

dr

(a - x)

1 о (а-ху2~\ -J

J гЗ

(с-2)2

dm dm

(57.2) (57.3)

Складывая полученные вторые производные, получаем

dW dW . dW п. дх Г ду ~ dzi ~

Уравнение (57.6) называется уравнением Лапласа.

(57.4)

(57.5)