Предположим теперь, что точка N удаляется в бесконечность. Потенциал Vn будет стремиться к нулю, а работа R будет равна потенциалу в точке М, т. е.

R = Vm (55.9)

Иными словами, потенциал силы притяжения в данной точке равен работе, которую необходимо совершить силе притяжения при перемещении единичной массы из бесконечности в данную точку*.

На основании (55.7) можно написать

(55.10)

т. е. производная от потенциала притяжения по любому направлению равна составляющей силы, действующей в этом направлении. Следовательно, из потенциала силы может быть получена ее слагающая по любому направлению.

Из уравнения (55.6) следует, что dV зависит от косинуса угла между направлением силы тяжести и направлением перемещения точки; отсюда следует, что потенциал V может получать приращение положительное, отрицательное и равное нулю.

Рассмотрим два предельных случая:

1. Если cos {F, s) = О, что соответствует перемещению точки под прямым углом к направлению F, то и работа силы будет равна нулю, т. е.

dF = 0. (.55.11)

Интегрируя (55.11), находим

F = nocT. = C, (55.12)

но F - функция координат х, у, z, поэтому (55.12) представляет собой уравнение поверхности, точнее семейство поверхностей, которые мы будем получать, давая С различные значения. Очевидно, эта поверхность может быть получена, если представить себе, что точка с единичной массой будет перемещаться во всех направлениях под прямым углом к направлению силы тяжести; в этом случае будет описана поверхность, обладающая свойством, что потенциал будет всюду сохранять постоянное значение.

Следовательно, поверхности, удовлетворяющие уравнению (55.12), обладают тем свойством, что сила притяжения в любой точке будет направлена по нормали к этой поверхности, а составляющие силы по касательной к поверхности в любой точке равны нулю. Такие поверхности называются уровенными.

2. Если cos {F, s) - 1, то это значит, что перемещение точки происходит по направлению действия силы, потенциал получает максимальное приращение и его выражение имеет вид

dVFds. (55.13)

Если же перемещение происходит в направлении, противоположном действию силы, то, очевидно, в этом случае

cos(F, s) = - 1

* Этот вывод справедлив не для всех видов потенциальной функции: в частности, он не применим к потенциалу силы тяжести.

dV=-Fds. (55.14)

Следовательно, знак приращения потенциала зависит от направления перемещения точки; в одном случае потенциал будет увеличиваться (приращение положительное), а в другом случае уменьшаться (приращение потенциала отрицательное).

Рассмотрим две бесконечно близкие уровенные поверхности, определяемые уравнениями V = С и V dV = (рис. 106). Допустим, что единичная масса переместилась из i5 в по направлению силы F. Тогда на основании (55.13) напишем

dV = Fds, (55.15)

но в данном случае ds представляет собой расстояние между взятыми уровен-ными поверхнастями. Обозначая это расстояние через dh, получаем

= F; dV=Fdh; dh = . (55.16)

Полученные выражения (55.16) соответствуют случаю перемещения точки по нормали к центру тела, т. е. когда

cos(F, s)= 4- 1.

При перемещении точки в обратном направлении, т. е. при cos {F, s) = -1, выражения (55.16) примут вид:

iI = F; dV-Fdh; dh-. (55.17)

Из равенств (55.16) и (55.17) следует, что расстояния между двумя близкими уровенными поверхностями в общем случае не равны в разных точках, а обратно пропорциональны силе, действующей в этих точках.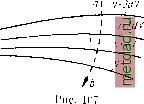

Pii.. 106

Из изложенного свойства потенциальной функции вытекает еще существенное обстоятельство. Пусть рис. 107 изображает сечение уровенных поверхностей, соответствующих уравнениям:

V + dV, F + 2dF, F-f3(F;

конечно, они, согласно (55.16), изобразятся кривыми, непараллельными между собой *.

Кривая аЪ пересекающая уровенные поверхности ортогонально, называется силовой линией. Иначе, силовыми линиями называются кривые,

* В данном и последующих случаях под непараллельными поверхностями будем понимать такие, расстояния между которыми, считаемые по нормали к одной из поверхностей, в различных точках разные.

касательные к которым совпадают с направлением векторов представляющих силу притяжения.

Выше установлены свойства, присущие потенциальным функциям, в том числе потенциалу силы притяжения.

Потенциалы силы притяжения объемных масс, кроме указанных выше, обладают еще иными важными свойствами; некоторые из них будут указаны /1;алее, после рассмотрения потенциалов притяжения некоторых простейших тел.

§ 56. Потенциал притяжения некоторых простейших тел

Найдем потенциал притяжения некоторых простейших тел. 1. Потенциал притяжения материальной точки выражается функцией (53.6), т. е.

(56.1)

2. Потенциал притяжения простого слоя на внешнюю материальную точку.

Допустим, что притягивающие массы заключены между двумя очень близкими поверхностями а и произвольной формы (рис. 108), расстояние между которыми равно Л. Если da - элементарная площадка на поверхности, то элементарный объем Ат выразится

Ат = h do.

(56.2)

Обозначая по-прежнему через б - плотность масс в этом элементарном объеме, получаем выражение его массы Am

Am = б/г. da.

(56.3)

Потенциал объемных масс, заключенных между поверхностями а и Ci, приближенно представится

V = fda, (56.4)

где г - расстояние элемента da поверхности до притягиваемой точки.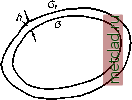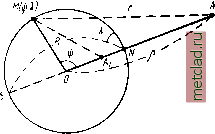

Рис. 108

Рис. 109

Будем неограниченно приближать поверхность к поверхности а, не изменяя при этом массу Am внутри каждого элемента объема Ат. В результате такого перехода на каждом элементе da будет сконденсирована масса dm.