притягивающего тела. Тогда величина г в выражении (53.15) может принять малые значения и стремиться к нулю. При г, стремящемся к нулю, его значение будет становиться величиной первого порядка малости. Следовательно, выражение

dn db dc г

будет величиной второго порядка малости. Первые производные от потенциала, содержащие интеграл вида

(53.19)

б da db dc,

в этом случае будут конечными и непрерывными, так как, если {а - х) будет стремиться к нулю, числитель станет величиной четвертого порядка малости, а знаменатель - третьего. Поэтому отношение их будет первого порядка малости.

Отсюда вытекает существенный вывод: потенциал притяжения Земли и его первые производные всюду конечны и однозначны; можно доказать, что они будут также непрерывными.

Введение понятия потенциала приводит к тому, что вместо получения и исследования трех функций, выражающих компоненты силы по осям координат, стало возможным находить и исследовать одну функцию. Выяснилось, что потенциальная функция обладает замечательными свойствами, использование которых оказалось чрезвычайно плодотворным для решения многих научных проблем, в том числе и проблемы изучения фигуры Земли.

§ 54. Разложение потенциала земного притяжения в ряд

Использование выражения для потенциала силы земного притяжения в виде

встречает известные трудности. Более удобное выражение для потенциала V можно получить путем разложения 1/г в ряд.

2 Примем систему пространственных прямо-

угольных координат с началом в центре Земли и с осью Z, совпадающей с осью вращения Земли (рис. 105). Тогда плоскость ху совпадает с плоскостью земного экватора.

Напишем выражение для потенциала притяжения

А(а,Ь,с)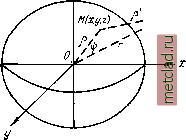

(54.1)

где р - расстояние притягиваемой точки А (а, Ъ, с) от текущей точки М (х, у, z) с элементарной массой dm. Обозначим расстояния от точек Л и М до начала координат О соответственно г и р.

(54.3)

С введенными обозначениями имеем:

р = (а - а:)2 + (6 -1/)2 + (с - 2)2 = а2 + Ь2 + с2 -

- 2{ax + by + cz) + x + y + z (54.2)

r2 = flr2-f Ь2 С2 p2 = x2+I/2 + z2

Тогда

р2 2гр + + р2 ,2 1 + + £i) . (54.4)

Из треугольника ОМА (см. рис. 105)

р2 = г2 -2rpcos\}) + p2. (54.5) Сравнивая (54.4) с (54.5), находим

=созур. (54.6)

Подставляя (54.6) в (54.4), получаем,

р 2 2 1 2 cos а) + . (54.7)

Для получения выражения входящего в (54.1), возведем (54.7) в сте-

пень-- и разложим правую часть по биному Ньютона, тогда получим ряд

по возрастающим степеням . I

Ограничиваясь членом с получаем

= I + Г + ii- 01) -1) + . ..]. (54.8)

Попутно укажем, что коэффициенты при степенях у являются так называемыми сферическими функциями, применяемыми в теории потенциала. Подставляя найденное значение в (54.1), находим

V = -dm + pcos->dm + p{Scosy-i)dm-\-.... (54.9)

Первый интеграл, распространенный на весь объем притягивающего тела будет равен его массе М.

Второй интеграл, принимая во внимание (54.6), можно представить так:

±poosdm==±.pdm + -Lpdm + -Lpdm. (54.10)

Но координаты центра массы тела (центра инерции) определяются формулой

f x dm

Аналогичные выражения получаются для других осей координат. Так как начало координат нами было принято в центре массы Земли, то х = 0. Принимая во внимание, что

ldm=:M, (54.12)

получаем

lxdm--=0. (54.13)

Аналогичные формулы получаются по другим осям координат. Тогда первый интеграл правой части (54.10) будет

J-.\pdm = J:j\axdm = xdin().

По тем же соображениям будут равны нулю и остальные два интеграла (54.10).

Следовательно,

J р cos ф dm. = 0. (54.14)

Таким образом, второй член разложения потенциала силы притяжения в ряд равен пулю.

Рассматривая третий интеграл выражения (54.9)

j р2 (3 cos2 y\>-i)dm 1- {ах+ cz)- р2 dm, (54.15)

замечаем, что при возведении в квадрат трехчлена {ах + Ьг/ + cz) появится, в частности, интеграл вида

ахЬу dm = аЪ ху dm. (54.16)

Интегралы вида J xydm называются произведениями инерции. При расположении координатных осей, совпадающих с главными осями инерции, они равны нулю. Поэтому (54.15) можно представить в виде

(аж -\-Ъу + czf - р2 cm = J (3 (ах- + bh/ + сЧ) - рV} dm =

= 7Г j (3 (а + + сV) - р2 ( 2 4 й2 , с2) dm. (54.17)

Соединяя вместе члены, содержащие а-, затем &2 разбиваем интеграл на три части, из которых первую напишем так:

-1- j а2 (32 -.p)dm = {2х - г/- z) dm. (54.18)

Аналогично две другие части представятся интегралами:

j (21/2 - 2-z2) dm, {2z-x-y) dm.

Из механики известно, что главные моменты инерции А, В, С относительно осей координат выражаются формулами:

A=]iy + z)dm I

Z? = j(x2 + 22)dm; C=\{x + y)dm ]