тических вычислений необходимо перейти от кривых oi, ok, ... к прямым, соединяющим конечные точки этих кривых. В направления ок и oi следует ввести поправки, равные углам между касательными к кривым, изображающим геодезические линии на плоскости, и прямыми, соединяющими конечные точки этих кривых. Эти поправки на рис. 83 изображаются углами ioV и кок и называются поправками за кривизну изображения геодезической линии на плоскости. Они обозначаются через Ь,

bok И Т. Д.

Дадим первоначально упрощенный вывод формул для вычисления этих поправок. Пусть на плоскости имеется изображение геодезической линии в виде кривой AaBx (рис. 84). Углы в точках Лж В, между касательными к кривой и хордой АВ обозначим через 6 2 и 63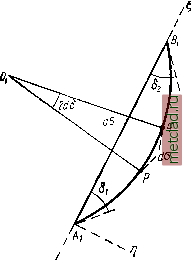

Рис. 85

Рве. 86

Координаты точек Л1 и В, обозначим через агц и а;2, У2 Если линия (iDi - изображение осевого меридиана, то

AiCx-Ух,

Фигуре ABCD на эллипсоиде (рис. 85) соответствует фигура AxaBxCJ), на плоскости. Сумма углов в фигуре ABCD на эллипсоиде равна 360° -f е. Сумма углов в фигуре AxaByCJ), на плоскости равна 360° + 61 2 + 62.1-

Вследствие конформности изображения суммы углов обеих фигур должны быть равны, т. е.

360*-f8 = 360 + 6i.2-f 62.1,

е = 61.2 + 62 1-

Полагая, 61 2 = Sg.i и принимая во внимание, что

е - (2 -аг) (yi + J/2) , * 8 2Я2 Р

* Выражение -i) iVi + У2) ддощадь трапеции АфСРх.

получаем

r - fi . £ (2 -ai) (У1 + У-?)

Обозначив

У1+У2

2 - f/m,

получим окончательно

б12 = б;1=-2р (43.1)

(не принимая во внимание знаков величин 2.1 как поправок).

Дадим вывод более точных формул. Пусть А уаВ (рис. 86) - изображение на плоскости геодезической линии АВ. Возьмем на кривой АаВ- две точки р и q, расположенные на бесконечно малом расстоянии одна от другой и ограничивающие участок dc. Для этого бесконечно малого участка разность х, - х обратится в dx, а

§1. 2 - 2. 1 - db.

Пусть Ох - центр кривизны для участка do. Угол pOq будет равен 2db. На основании (43.1) имеем

2db=y,

Обозначив радиус кривизны кривой АаВ через р, напишем из треугольника pOq

2 dbp = da,

или на основании (42.1)

2d6p = dS, (43.2)

где dS - элемент хорды АВ. Из (43.2) получим

i 2dd у dx ,0 ov

J-~ds -ЖЖ

Возьмем систему координат с началом в точке А j; ось направим по хорде ABxi а осьт] - по направлению, перпендикулярному к ней. Напишем выражение, известное из дифференциальной геометрии, для радиуса кривизны

1= /!!..-,., (43.4)

Величина щ - тангенс малого угла между кривой АаВ и хордой АВх, квадрат этой величины будет ничтожен по сравнению с единицей, с которой он складывается в выражении для Поэтому приближенно можно написать

1 d-r

На основании формул (43.3) и (43.5) напишем равенство

й2т] у dx

(43.5)

Так как ось направлена по хорде ЛВх, то

dS=dl.

Обозначив координаты точек Аж В, через х у, и х, г/а а дирекционный угол хорды АВ, - через Г, будем иметь

x = x-,-\-tcosT: у r=u,-\-sinT

dx = с? cos Г

Принимая во внимание последние выражения, получаем

Интегрируя последнее уравнение и считая В постоянным, равным R,ni получаем:

-f = - + -4s-cosr+C (43.7)

В написанных выражениях С-жС - произвольные постоянные. Определим лх. Так как в точке А,

то из (43.7) находим а из (43.7)

1 - - 1 2

С2 = 0.

В точке Bj ордината ц =0, = 5 = ЛВ, поэтому из формулы (43.7) имеем

yicos г 5 ,

0 = -у --sinrcosr-6i.2,

откуда

0 г/1 cos Г р , 52 .

01 2 = --5- Ч--г-Sin Г COS Г,

или, учитывая (43.6), получаем:

R г/1 (Ж2 - хх) , (Х9 - жх) (у2 - yi)

R - (2-1) {I У2-УХ \

2 = (2- l) (г/-- . (43.8)

1.2 = 7 (22- i) (2г/1+ г/2). (43.9)