Глава V

ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМУЛЫ

§ 33. Дифференциальные формулы первого рода

После обработки триангуляции и вычисления геодезических координат пунктов может оказаться, что начальные данные (длина и азимут исходной стороны, координаты начального пункта), принятые при обработке, подлежат небольшим изменениям. Это, естественно, вызывает необходимость исправления всех вычисленных широт, долгот и азимутов триангуляции. Конечно, можно заново решить треугольники и вычислить широты, долготы и азимуты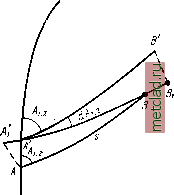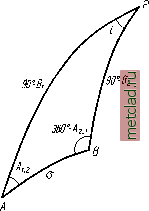

Рис. 63

Рис. 64

на основе новых исходных данных, однако проще исправить координаты пунктов путем вычисления поправок к ним.

Формулы, выражающие поправки геодезических координат пунктов и азимутов направлений за изменение начальных данных триангуляции, называются дифференциальными формулами первого рода.

Бывают случаи, когда необходимо изменить параметры принятого референц-эллипсоида. Это может случиться при использовании старых триангуляции, которые относились в России к эллипсоидам Вальбека, Кларка, Бесселя, тогда как в настоящее время в СССР принят эллипсоид Красовского. Кроме того, в связи с переходом к эллипсоиду Красовского возникает необходимость перевычисления координат пунктов на этот эллипсоид, так как в старых каталогах приведены координаты пунктов, вычисленные с использованием параметров эллипсоида Бесселя, который был принят в геодезических работах СССР до 1942 г. Конечно, координаты, отнесенные к новому эллипсоиду, могут быть получены путем перевычисления координат пунктов с использованием новых значений параметров референц-эллипсоида. Однако и в этом случае проще получить новые координаты пунктов путем вычисления и введения поправок за изменение параметров эллипсоида.

Формулы, выражающие поправки геодезических координат за изменение параметров эллипсоида, называются дифференциальными формулами второго рода.

Выведем дифференциальные формулы первого рода.

Пусть в результате ранее выполненных вычислений получены геодезические координаты конечных точек стороны триангуляции АВ (см. рис. 62), ее длина, прямой и обратный азимуты.

Обозначим:

Bi, Li - координаты пункта А; В2, L2 - координаты пункта В; Ау 2 - азимут с А на Б; Л2.1 - азимут с Б на Л; S - расстояние АВ. Пусть широта пункта А изменилась на малую величину dB, азимут и длина линии АВ - на малые величины dA 2 и ds соответственно. Найдем выражения для поправок в координаты пункта 5 и в обратный азимут Л 2. i, т. е. dB2, dL2 и da. 1 как функции изменений 5, 2 и ds. Учитывая, что 2 и б?5 - малые величины, имеем:

dB2 = dB,.

дВ.2

dL2 =

dA2.1 =

дА2.1

dAi 2

ds (9i 2 dA2, 17 , dA

dA-x 2

dAi 2+ dLi

dBi ds dAi 2

dL2 = dLi + cZLf Ч- dL\ + dbf- 2 dA2. r = dA\ 1 +dA\

dAi,

(33.1)

(33.2)

1. В Ы в 0 Д в e л и 4 и H dB\ dL и dA\. Пусть точка А, лежащая на меридиане точки А (рис. 63), имеет широту B--i- dB,. Будем поворачивать геодезическую линию В А вокруг точки В до тех пор, пока она не пройдет через точку А\ Точка А переместится в положение А[. Перемещаем точку А[ (в положение А, сохраняя при этом длину линии АВ, равной s. Тогда точка В переместится в положение В, и, очевидно, АВ\ = 5. Будем поворачивать линию АВ вокруг точки А до тех пор, пока ее азимут не сделается равным А -у з , при этом В[ переместится в положение В. Очевидно, разность широт точек В и В получится

т. е. это будет часть поправки йБд, обусловленная изменением широты точки А на величину dB,.

Из рис. 63 имеем:

551 = ЛЛ = Ml cos Л1.2,

AA{ = MydBy sin Л г. 2-

Применяя формулы для решения прямой геодезической задачи, получаем разность широт точек В[ ж В

MxdBxCos Ау 2 cos/4 2 1

Ж7 -

а разность широт точек В и равна

Ml dBi sin Ai 2 sin A, i

Так как AAi BiB% следовательно,

T B, MidBiCOsAi 2 cos/I? 1 MidBisinAi 2sino i

ав - Щ-=---Щ-

dBl = -(5i(cos 2C0S 2. i + sin 1 2sin2.1). (33.3)

Из треугольника АВР (рис. 64), который мы рассматриваем как сферический,

cosZ = -cosAi 2 cos Л 2.1 - sin Ai 2 sin Л 2. i cos a. (33.4)

Полагая в выражении (33.4) cos a = 1, на основании (33.3) и (33.4) получаем

dB = -f cos Z dBi. (33.5)

Для вывода dLf* заметим, что

L2 = Li + l; dL2==dLi + dl; dl = dl +dl + dl-. По аналогии с предыдуш,им

jjBi Ml cos Л1 о sin Л2. 1 , Ml dZ?! sin Л1. 2 cos Ло. 1

N.2 cos B2 iV2COSi52 ~

dzf =-- (cos Лх 2Sin2 1 -sini aCosa Л dBi. (33.6)

Ho из рис. 64 имеем:

sin 2 sin Z = -sin Л 2. iCos 2 +cos Л 2. isinyli, 2 cos a, -sin Bgsin Z - cos yli , if 2.1 -sin Л j 2 cos Л2.1 cos a.

Положим, что cos 0=1, тогда формула (33.6) примет вид

dl=smUgB2dBi. (33.7)

Для вывода dAzi вспомним, что

Ло 1-Л1.2±180° + ,

следовательно,

dA2 i=dt. (33.8)

Из треугольника сРЪ (рис. 65)

sin В2 - ctg Z tg

tg = tg Z sin B2. Дифференцируя (33.9), находим

-- = , sin Bo + tg I cos Bo dBo.

C0S2 г C0S2 I 2 I S 2 2

(33.9)