По способу Бесселя задача решается по следующему плану:

1. Треугольник АРВ (рис. 54) переносится на шар по заданным трем элементам треугольника при помощи основного уравнения геодезической линии

cos wsin Лх 2 = сод 2sin л 2.1 = с. (29.1)

2. После указанного перехода полученный на сфере треугольник АРВ (рис. 55) решается относительно известных его элементов.

Зппипсоид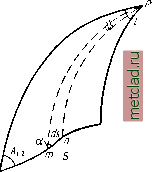

f\iBj.L,)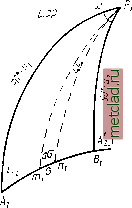

Рис. 54

Рис. 55

3. От вычисленных из решения сферического треугольника элементов осуществляется переход к соответствующим элементам сфероидического треугольника.

Остановимся подробнее на переходе от сфероидического треугольника АРВ к сферическому АРхВу.

Если обозначим элементы сферического треугольника так, как показано на рис. 55, то уравнение геодезической линии (29.1) представит собой одновременно точную зависимость, вытекающую из теоремы синусов для этого треугольника

sin Ах 2

sin (180° -/12. i)

(29.2)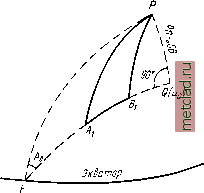

Рис. 56

Sin (90° -Из) sin(90° -ui)

Отсюда можно установить соотношения и соответствия между элементами сфероидического треугольника АРВ и сферического хРгВх.

1. Стороны АхРх и ВхРх на сфере равны дополнениям до 90° приведенных широт точек Л. и Б на эллипсоиде, т. е. 90 - и 90 - и точка Pi на шаре играет роль полюса. Согласно (4.27), приведенные широты и определяются по формуле

lgu==Yi - eXgB.

2. Геодезическая линия s на эллипсоиде между точками А и В соответствует на сфере дуге большого круга а, на которой в каждой ее точке азимуты равны азимутам геодезической линии в соответствуюш;их точках на эллипсоиде. Следовательно, углы сфероидического треугольника АРВ в точках А ж В равны углам сферического в точках и В х-

Эти зависимости однозначно определяют элементы сферического треугольника АРВ.

В дальнейшем (для упрош;ения) радиус сферы будем считать равным единице.

Укажем попутно геометрический смысл постоянного с в уравнении (29.1). Если продолжим дугу большего круга до экватора в точке F (и = 0) и до пересечения в точке Q с меридианом, составляюш,им с дугой угол 90° (рис. 56), то получим:

для точки F с = sin Л о,

Q с = cos uq.

Для получения фор.мул решения задачи по способу Бесселя необходимо установить зависимость между разностями долгот пунктов на эллипсоиде и на шаре, т. е. между Z и со, а также между длиной геодезической линии на эллипсоиде s и дугой большого круга с на шаре.

Ход вывода формул для решения главной геодезической задачи по способу Бесселя:

1. Вывод дифференциальных уравнений, устанавливаювдих связьмежду S и а, Z и со.

2. Интегрирование полученных дифференциальных уравнений.

3. Решение треугольника на сфере применительно к условиям прямой и обратной задачи и окончательное вычисление определяемых величин.

1. Вывод дифференциальных уравнений

Обозначим (рис. 54):

ds - бесконечно малый элемент геодезической линии s на эллипсоиде; а - азимут элемента ds\ В ж и - геодезическая и приведенная широты текугдей точки ттг; du ж dl - разности широт и долгот точек т ж п. На рис. 55:

do = т-хп-х - бесконечно малый элемент дуги большого круга на шаре соответствующий элементу ds на эллипсоиде; dcd - разность долгот точек и п- на шаре. С этими обозначениями:

du = do cos а, MdB = ds cos а,

откуда

dB ds

=М4-. (29.3)

На основании (4.28) и (4.29) напишем:

Я1П7/= -, (29.4)

У1 -e2sin2£

г, У1-e2cosu /пп с\ VI -е2 cos2 и

откуда

J i/l-of COS Б , e2sin2 5cos5 1 /on/э\

cosda= Т/1 -r .=T--- 7-[ 5 (29.6)

/1 -e2sin2 (1 -e2 sin2 5)*/

du Vi - e2 cos В

dB cos u (1 e2sin2 5)*

Из (29.5)

cos Б Vi-e

cosu /i e2cos2w

(29.7)

(29.8>

тогда, принимая во внимание (29.8) и умножая числитель и знаменатель в (29.7) на а, получаем

du а (1 -е2) 1

dB ~ о (1 -е2 81п2Б)/ /1 -e2cos2u

ИЛИ окончательно

du м

dB а ]/1 - е2 cos2 и

На основании (29.3) и (29.9)

М 1 da

(29.9)

а /l -e2cos2u

откуда

= а 1/1 - е2 cos2 са. (29.10)

Далее, из рис. 54 и 55 имеем:

dod cos и = do sin а N cos Bdl- dssm a Откуда в результате деления получаем

NCOS В dl ds

(29.11) (29.12)

cos и d(0 do Принимая во внимание (29.10),

N cos Bdl = а cos и У 1 - cosu d(o. Учитывая (4.22), получаем окончательно

dl = Vi-ecos иd(i). (29.13)