При выводе будем следовать указанному выше общему порядку решения задачи.

1. Переход от исходных данных на эллипсоиде к соответствующим им величинам на шаре. Пусть на эллипсоиде (рис. 51):

By и В2 - широты точек А ж В; А-у2 и 2.1пряо и обратный азимуты геодезической линии АВ\ I - разность долгот точек А я В; S - расстояние между точками А ж В. Пусть точки Л 1 и By - изображения на шаре точек А и В эллипсоида, имеющие широты и С72-

Нормальную широту на шаре примем Un =

Проведем па-

0 2

рал л ели ВПуИ EF через точки и Ci на шаре, тогда точки Еж будут точками пересечения последней параллели с меридианами АР и ВР- Пусть точка С на эллипсоиде соответствует точке Ci на шаре, т. е. точка - изображение на шаре точки С. Проведем параллель через точку С, и пусть точки Е ж F - пересечение параллели с меридианами АР ж BP. Так как параллели на эллипсоиде изображаются параллелями на шаре, то точки Е-, Fi, будут изображениями точек Е, F, D.

Широта параллели EF - нормальная широта Bq на эллипсоиде. Так как разности В - Bq ж В2 - Bq для сторон триангуляции не превышают i°

-g-, ТО, согласно (28.13), масштаб изображения в пределах зоны расположения

дуги А В можно считать постоянным и рав-Вым единице. Иначе говоря, все линейные элементы в пределах треугольника ABD переносятся на шар практически без искаже-яий, в том числе и длина стороны Л 5 = S, являющаяся одной из исходных величин для решения задачи.

Имея это в виду, можно написать AExExDx==AE = ED.

Возьмем на меридиане АР точку Н, имеющую широту

2 Рис.51

Понятно, что точки Н ж Е же совпадут: точка Е располагается посередине дуги AD, т. е. на одинаковом линейном расстоянии от точек Л и £) по дуге меридиана; точка же располагается так, что разности Лхирот между этой точкой и точками Л. и 1)одина-* о в ы. Вследствие разницы в кривизне меридиана точка Н будет находиться на разных линейных расстояниях от точек Л и D.

Найдем разность широт точек Н ж Е, т. е. В - Bq.

Напишем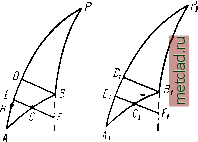

Bi 4 в 2

6 = 2-61.

Применяя формулу (25.11) для Ъ, получаем

В, Bl + (1 - -f .2 sin 2Bi ) . (28.16)

Для вычисления широты Bq воспользуемся той же формулой (25.11), так как точка Е, имеюш;ая широту В q, расположена на расстоянии от

точки А. Заменяя в этой формуле и = s cos А через b через ~, получаем

0 = 1 +1 Р (1 - Т -) . (28.17) Сравнивая (28.16) с (28.17), находим

B -B = -±.esm2B,Jf. (28.18)

Для Ь = 1300 (что соответствует расстоянию s = 40 км) при широте В = 60° получим

B -Bq<J,

Такое малое расхождение между В и В позволит в дальнейшем не отличать радиусов Mq и Nq, вычисленных для широты В о, от радиусов и Мщу вычисленных для широты В-

Поправка в азимут за переход от изображения геодезической линии на шаре к дуге большого круга при настоянием выборе нормальной широты и при S 60 км будет пренебрегаемо мала.

Таким образом, при расстоянии s между пунктами Л и В, не превышающем 40 км, и указанном выборе нормальной параллели два элемента треугольника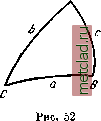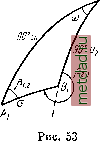

АВР - сторона АВ = s, и азимут А. - переносятся на шар практически без заметных искажений. При этом за нормальную широту на эллипсоиде для стороны А В следует принять

Вт =

В1 + В2

Сферический треугольник АВР решают по особым формулам, в которых в качестве третьего исходного элемента участвует Uq = . Зависимость

между Со и соответствующей втиротой Bq (или, как показано выше, широтой В = -1 + ) определяется на основании (28.10)

sinC/o=.i. (28.19)

Решение сферического треугольника. Для треугольника ABC (рис. 52) имеем формулы Гаусса:

. а С -В

sm -у COS ---

. а . С-В sm--sm ---

. с+Ь . А sin --sm

sm --- cos

2 А

а C-i-B c + b .

COSCOS-- = cos--sm

a . C+B c-b A

COS -g- sm -- = cos -2- 2~

(28.20)

Применим эти формулы к решению треугольника (рис. 53). Обозначим:

Ui W. U2 - широты 1 и

© - разность долгот этих точек;

0 - расстояние АВ но дуге большого круга;

Pi.2 и р2.1 -прямой и обратный азимуты дуги АВ-

Тогда

й = а; С = & = 90-Z7i; Л-со; c-OO-t/.; 5 = 360*-P2.i.

Кроме того, обозначим:

JIi±£1-=Uq; U2-U,==q: Р2.1 = Р2.1-180; iiljliii р, ;

Р2. 1-Pl.2 = .

Формулы (28.20) с принятыми обозначениями примут вид:

sin sin rti = sin cos f/oi

sin -J- cos = cos -y sin --,

cos sin -y = sm -Y sm (7,

COS cos = COS cos --.

Раскладывая синусы и косинусы малых дуг в ряд, получаем: а (l --)sinp = (u (1 -cos С/о

c(l-)cosp = ,(l-)(l-i)

(-+)(-#)= i-S-)°

(28.21)