Если обозначим через Uq широту на шаре, соответствуюш;ую нормальной широте Во на эллипсоиде, то математически условие первое выразится так:

R cos Un . /по о\

о=о = а=1.. (28.8)

где и о - масштаб изображения на параллели под широтой Во-

Для математического выражения второго условия напишем сначала выражение для масштаба в виде

-0+ [-dTjo- + -2-+ [-ш)о-6-+

где В - широта текуп];ей точки, находяш;ейся на расстоянии В - Во от нормальной широты.

С учетом (28.8) напишем

-=1+().( - .)+().+().+---

Условие медленного изменения масштаба при удалении от параллели с широтой Во целесообразно выразить так:

(). = 0 (w). = 0- (28.9)

Выражения (28.8) и (28.9), даюш,ие три уравнения, позволяют определить три постоянные. Находим производные (28.9), учитывая (28.8), и совместно решаем три полученных уравнения; после соответствуюш;их преобразований получим:

sin Bq

sin Uq -a2 1 +

e2 cos4 Bq 1 -e2

(28.10)

ir- U 2 ; (i-esinBQ\- .98 11 --tg(-- + -L) U + .sinBoJ

RYM (28.12)

Из (28.12) следует, что радиус шара равен среднему радиусу кривизны эллипсоида в точке с широтой Во-

В математической картографии, когда стоит задача изображения всего :эллипсоида на шаре, принимают L = (o, т. е. а = 1, А; = 1 (что означает совпадение плоскостей экваторов эллипсоида и шара) и

В а 1--sin В или R =а.

При условии (28.9) легко найдем выражение масштаба т

Вычисляя получаем в логарифмическом виде

l m~ 2 g2 (l e2)sinBoCOsBo /D n 43 OQ.AW

\gm----(l--e2sin2Bo)2--(B-Bof. (28.13)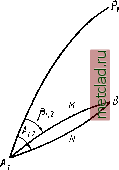

Рис. 50

Для (Б - So) = 1 и Бо = 55°

lgm = 0.000 00001.

Отсюда можно сделать весьма важный вывод: в пределах зоны, ограничен-1° 1°

нойБо - 1-jh5o + 1-,t. е. в пределах пояса шириной до 250 км, практически масштаб можно считать равным единице при указанном выше условии выбора постоянных.

Этот вывод исчерпываюш;е показывает выгоду использования поверхности шара для проектирования поверхности эллипсоида и малую величину искажений, обусловленную незначительностью сжатия земного эллипсоида.

Таким образом, если триангуляционная сеть расположена на расстоянии 100-120 км к северу или югу от параллели с нормальной широтой (и, конечно, как угодно далеко по долготе), то можно считать, что элементы триангуляции на эллипсоиде переносятся на шар без искажений: угловые - по конформности проекции, а линейные - по малости искажений. Этим обстоятельством мы воспользуемся при выводе формул для решения геодезической задачи.

Однако в азимуты приходится вводить поправку, хотя проекция и конформна. Дело в том, что геодевическая линия на эллипсоиде изображается на шаре кривой, не совпадающей с дугой большого круга.

Пусть на рис. 50 кривая AyNBi - изображение геодезической линии АВ si шаре; эта кривая будет двоякой кривизны. Азимут ее в точке А ио кон-

tpMHOCTH изображения в точности равен азимуту А геодезической линии эллипсоиде. Пусть АМВ - дуга большого круга, соединяющая точки Ai и By- Чтобы в дальнейшем иметь возможность пользоваться формулами сферической тригонометрии, необходимо в азимут кривой ANB ввести поправку, равную разности азимутов кривой ANB- и дуги большого круга AjMB. После этого треугольники на шаре будут иметь стороны, являющиеся дугами больших кругов. Однако вследствие близости земного эллипсоида к iliapy эта поправка вводится лишь в значения направлений, конечные точки которых расположены на расстоянии более 50-70 км от параллели с нормаль-нбй широтой Б Q. При расположении точек на меньших расстояниях этой поправкой можно пренебречь.

Упрощенные выражения для {А - Р):

1.2- Pi. 2=S sin Л1. 2 (1±) ,

А 1- Р2. 1= - sin 2 (-) . (l-e2sin2Bo)

i = l, 2.

При удалении пунктов триангуляции от параллели с широтой Bq более чем на 1° (110 км) следует учитывать линейные искажения.

Если обозначить через ds элемент геодезической линии на эллипсоиде в точке А, а через dS - элемент дуги большого круга на шаре, то

т = -3-,

-откуда

5=jmcZs, (28.14)

Подставляем в (28.14) значение т и интегрируем; после преобразований получим

lg5=.lg.+ li±lii, (28.15)

где т-х Т1 - масштабы изображения в точках А ж В.

Решение прямой геодезической задачи с применением Гауссовой теории изображения эллипсоида на шаре. В качестве иллюстрации применения теории Гаусса к задачам высшей геодезии выведем формулы для решения прямой геодезической задачи, которые получены в § 26. Обш;ий ход решения задачи состоит в том, что исходные данные В, L, А i отнесенные к поверхности эллипсоида, переносятся на шар по закону конформного изображения эллипсоида на шаре. Задача решается на поверхности шара, в результате чего определяются широта, разность долгот и обратный азимут на шаре. В соответствии с тем же законом изображения осуш;ествляется обратный переход с шара на эллипсоид, в результате которого и определяются искомые величины: широта В2, разность долгот I и обратный азимут А з. i.

Задачу можно решать двумя способами: 1) путем перехода от числовых значений исходной широты, азимута и длины стороны на эллипсоиде к соответственным числовым значениям этих же величин на шаре, решения сферического треугольника с числовыми данными и обратного перехода с шара на эллипсоид также с числовыми данными; 2) переход с эллипсоида на шар, решение сферического треугольника на шаре и обратный переход с шара на эллипсоид осуществляют в процессе вывода формул в общем виде, а не с числовыми данными задачи. В этом случае шар используется как промежуточная поверхность при выводе формул, выражающих искомые разности широт, долгот и азимутов. Элементы сферического треугольника, которые появляются в процессе вывода формул, исключаются, и окончательные формулы выражают зависимость между данными и искомыми величинами на эллипсоиде.

Первый способ вследствие громоздкости на практике не применяется. Второй способ довольно часто находит применение, поэтому ниже он изложен ,с необходимой подробностью. При выводе формул будем иметь в виду их применение для вычисления координат по сторонам треугольников триангуляции, т. е. для расстояний, не превышающих 50 км.

Вывод формул для второго способа, данный Гауссом, основан на разложении в ряды искомых величин. Приведем вывод этих формул, предложенный проф. Ф. Н. Красовским. Этот вывод основан на геометрическом подходе; он прост и в то же время отчетливо показывает достоинства использования конформного изображения эллипсоида на шаре для решения геодезической задачи.