причем ось z расположена по оси вращения эллипсоида ОР, а оси х ш у находятся в плоскости, перпендикулярной к оси ОР (первая система координат); пусть А а - элемент геодезической линии, имеющий длину ds и азимут а. Проекция элемента ds на параллель, т. е. отрезок АЪ, равна ds sin а.

Так как точка а находится на бесконечно малом расстоянии от А, то координатами точки а будут х -{- dx, у -Ь dy, z + dz, а ее проекции на плоскость параллели точки А, т. е. координатами точки d, будут х dx; у dy ш z. Радиус параллели точки Л, равный Л С = 6С, обозначим через г.

Определим площадь треугольника AdC = Р, изобразив его отдельно на рис. 28,

Р = Y {(г (уdy) - ху-2xdy-dxdy},

Р -={у dx-xdy).

Площадь сектора АЪС (см. рис. 27) будет равна -rds sin а.

При бесконечно малых dx и dy площади треугольника AdC ж сектора АЬС равны между собой, поэтому

-{у dx-x dy) = -rds sin a,

или, по (14.4),

С ds - rs\n.ads,

откуда

г sin a = С, (14.5)

а COS а sin а = с, (l-i

т. е. получили уравнения (13.8) и (13.9).

§ 15. Расхождение взаимных нормальных сечений

Возьмем на поверхности эллипсоида две точки А ж В, имеющие разные широты и долготы (рис. 29). Обозначим:

п, щ - точки пересечения нормалей к поверхности эллипсоида в точках А и В с малой осью; а - угол между прямыми пА и пВ; АаВ - прямое нормальное сечение в Л на точку В; ВЪА - прямое нормальное сечение в Б на точку А\

АВ - хорда - линия пересечения плоскостей прямого и обратного сечений АВп и АВщ; г - угол пВщ.

Для определения отрезка njifj воспользуемся формулами (11.2) и (11.3), из которых получим (см. рис. 17 и 29):

Оп = ае Sin Bfi+Y sini) , Опь = ае-&т Bg ( 1 + j е- sinBa)

lirri

Следовательно, с ошибкой порядка ае {В - В можем написать: = Ощ - Опа = ае (sin В< - sin 5),

щпь = ае{В2 -В cos В, (15.1)

Отметим, что треугольник Л тгБ можно считать равнобедренным, так как

Апа Вп, следовательно, угол АЬп приближенно равен 90° - . Обозна-

чим через / угол между плоскостями АВп и АВп двух взаимно обратных нормальных сечений. Приняв за центр точку В, построим сферический треугольник АпаПь, соответствуюш;ий трехграннику с ребрами ВА, Вщ, Впа (рис. 29 и 30). В этом треугольнике стороне ПаЩ будет соответствовать угол г, стороне

Апа - угол АВПа, равный 90° -

Угол при вершине треугольника А будет искомым утлом /, а угол при] п,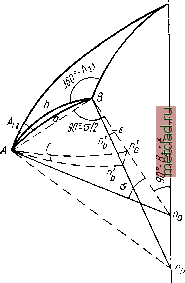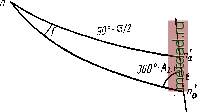

Рис. 29

Рис. 30

равен 360° - Л 2.1, так как плоскость, проходящая через точки В, Wq, есть плоскость меридиана точки В. Из треугольника АпсРь имеем

sin /

sin (360°-Л2.1)

(15.2)

sin (90°-1)

Из треугольника Впщ (см. рис. 29) следует

sin £ пдпь

sin (90°-52 + S) ~~ No

Заменяя щп, согласно (15.1), и пренебрегая в знаменателе левой части последнего уравнения величиной е, получаем

sin 8 ае2 (В2 - i) cos Вщ

cos i?2

©ткуда

ae2 (Д -jji) cos B2 cos Вт

Sine--.

или с ошибкой порядка е* {В - bi)

sin 8 = {В2 - Bi) cos В2cos В.

На основании (15.2)

(15.3)

sin/ =

sine sin Л2.1

или, принимая во внимание (15,3) и заменяя cos В 2 на cos В, получаем

е2 (Bz-B-i) cos2 вт sin Л2.1

sin у - - ,

Но приближенно

(В2-Bj)=5 COS 1 2(1)1 cos л

Полагая А 2,1= А 1,2±180°, получаем, пренебрегая ошибкой порядка еа 2,

/ = еа cos Л cos2 В sin Л i зр ,

/ = i. eG cos2 В sin 241.2Р . При s = 100 км, о В,п = 45° и А 1.2= 45°:

(15.4)

Таким образом, / - угол между плоскостями взаимных нормальных сечений - величина малая второго порядка. Для максимальных длин сторон треугольников триангуляции 1 класса, равных 40-50 км, значение /* равно 2-3*. Следовательно, угловые и линейные рас-/р хождения между взаимными нормальными сечениями будут величинами малыми. Поэтому при последуюш;ем выводе фор-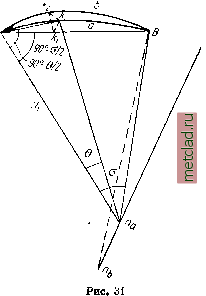

Рис. 33

мул можно дуги АаВ и АЬВ рассматривать как сферические с центром в па

или пу.

На рис. АаВ - дуга прямого нормального сечения в точке Л, рассматриваемая как дуга окружности с центром в АЬВ - обратное нормальное