Докажем важную теорему для геодезической линии: произведение радиуса параллели на синус азимута в каждой

точке геодезической линии - величина постоянная, т. е.

г sin А ~ const.

Изобразим меридиан точки А в плоскости чертежа (рис. 26). Если радиус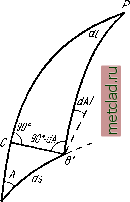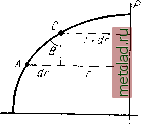

Рис. 25

Рис. 26

параллели точки А обозначить через г, то радиус параллели точки С будет г -\- dr, причем по чертежу для dr будем иметь

-dr = MdB sin В. Из уравнений (13.1) пишем

cos А=М

5ША=Г

dB ds *

(13.5)

(13.6) (13.7)

Помножим левую и правую части уравнений (13.6) на rdA, а уравнения (13.7) на dr и сложим. Будем иметь:

Г COS AdA = Mr -т- sin В dl

drsmA = rdr4 = -Mr-dBsinB

ds ds

равен

г cos A dA~{-dr sin A =0. В правой части мы получили полный дифференциал, интеграл которого

г sin Л = const. (13.8)

Следовательно, теорема доказана. Согласно (4.21),

r = acosii,

поэтому уравнение (13.8) может быть переписано

acoswsln=c (13.9)

cos sin Л1 = cos 1*2 sin Лд = . . . = с.

Из уравнения (13.9) следует, что для геодезической линии на поверхности эллипсоида вращения произведение косинуса приведенной широты точки геодезической линии на синус азимута геодезической линии в той же точке есть величина постоянная.

Уравнения (13.8) и (13.9) представляют собой два вида основного уравнения геодезической линии на поверхности эллипсоида вращения.

Эти уравнения в дальнейшем будут использованы при выводе формул для вычисления геодезических координат при больших расстояниях между пунктами.

§ 14. Аналитический вывод основного уравнения геодезической линии на поверхности вращения

Учитывая большое значение, которое имеет геодезическая линия в высшей геодезии, в этом параграфе получим общий вид дифференциального уравнения геодезической линии на любой поверхности исходя из ее определения и, далее, как частный случай, получим уравнение линии для поверхности эллипсоида вращения.

Пусть имеем поверхность, уравнение которой

F{x, у, z) = 0.

Параметрическое уравнение геодезической линии в общем виде будет

xf{s); г/ = ф(5); z = {s), (14.1)

где s - длина геодезической линии.

Известно, что косинусы углов а, §, v> образуемых нормалью к поверхности с осями координат, будут равны:

др OF дР

cosa -cos (5 = -; cosy =

Известно также, что косинусы углов, образованных главной нормалью к кривой с осями координатору, jv, y)v, равны

cosa2v = i?4; cosp2v = i?4S-*. COSYiV =

d2z

ds2 *

где r - радиус первой кривизны.

Геодезическая линия определяется как кривая на данной поверхности, в каждой точке которой ее соприкасающаяся плоскость проходит через нормаль к поверхности в той же точке; это определение равносильно требованию совпадения главной нормали кривой в каждой ее точке с нормалью к поверхности в той же точке (главной нормалью кривой называется прямая, полученная в результате пересечения нормальной и соприкасающейся плоскостей, относящихся к одной точке кривой). Это совпадение произойдет, если

дР дР дР

дх .р dx , ду г> d , D dz

Z) I ds2 D ~ ds2 D ~ ds-

OF дх

= RD;

d-y ds2

OF dz dz ds-2

= RD.

Следовательно, уравнение геодезической линии для произвольной поверхности имеет вид

(14.2)

ства на поверхности земного эллипсоида, являющегося поверхностью вращения. Р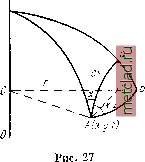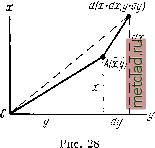

Это уравнение будет частным случаем уравнения (14.2). Напишем уравнение поверхности вращения в виде

ж + г/ + /(2) = 0.

Соответствующие частные производные, входящие в (14.2), будут равны:

(14.3)

Следовательно, уравнение геодезической линии на поверхности вращения, согласно (14.2) и (14.3), будет иметь вид

2х 2у fjz) dx dy dz

ds2 ds2

Интегрируя, получаем

dx ds2

dy ds

(14.4)

-{-у dx - xdy - С ds,

где С - постоянная интегрирования.

Определим геометрический смысл выражения Cds. Пусть координаты точки А (рис. 27), расположенной на поверхности эллипсоида, равны х, у, z,