Введя вектор т направляющих косинусов линии МС

тЛ /cos б cos а\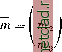

cos 6 sin а Vsin б

запишем уравнение (110.2) как

Нс = Вм + г-т,

(110.3)

(110.4)

где г - длина вектора г .

Считая, что приближенные положения точек М и С известны, получим формулы, связывающие поправки к приближенным координатам Rq и R, для чего дифференцируем уравнение (110.4):

dRc = dHM + r dm + m-dr. (110.5)

Дифференцируя уравнения (110.3), получим

dnii = -(cos а sin б) dd - (sin а cos б) da dm2=~(sina-sin6)-d6 + (cosa-cos6)-dct i. (110.6)

drus = cos 6 db

Теперь система уравнений (110.5) может быть записана в виде dXc - dXfn = -г cos а sin б d6 - sin а cos б da* -f- cos a cos 6 dr, dYс - dYm = -f sin a sin 6 db* -fr cos a cos 6 da! + sin a* -zosb* -df, dZc = dZm = r cos 6 d6 + sin 6 dr

/dXc - dXfn\ /-r cosa sin6 -r sin a cos 6 cosa-coseX /db\

da \, KdrJ

dYc-dYm \dZc - dZml

-f sin a sin 6 \ f cos 6

r COS a cos 6 0

sin a cos 6 sin 6

,dXc - dXm\ dYc-dY,

\dZc-dZmJ

/-cosa Sine* -sin a sin 6

cos 6

-sin a cos a-cos 6 cos a sin a-cos 6

0 sin 6

\ / db \ cos 6 da: dr

Запишем уравнение (110.5) как

dRc-dRm = r-QT.dJ, I-cos a-sin б -sin a cos acos 6

(110.7)

-sin a* sin 6 cos 6*

cos a sin a cos 6 0 sin 6 .

dl =

db \ cos 6 da

Нетрудно убедиться, что

QT.Q = E.

Тогда, умножив уравнение (110.6) слева на -Q, получим

( db

cos а da

d - Q-mc-dR)

-cos a-sin б -sin a-sin б cos б -sin a cos a 0

\ cos a cos 6 sin a cos 6 sin 6V \ dZr - dZn,

/dXc - dXm\ dYc - dY,

(110.8)

(110.9)

Уравнение (110.8) и является основным уравнением космической геодезии, так как оно дает связь измеряемых топоцентрических координат а, б, г с определяемыми параметрами dRc и dR (последние можно рассматривать как поправки к приближенным значениям координат наземных станций и положений спутника).

При численном решении уравнений (110.9) величины db, da, dr полагают равными разностям между измеренными значениями и значениями, вычисленными по приближенным координатам точек М и С, т. е.

db = бцзм бвь1Ч

da = Оизм Овыч dr = г изм - выч

(110,10

Если измеренных величин больше, чем определяемых параметров, то последние оценивают статистически.

Если координаты R точки М известны, то основное уравнение принимает вид

de = -QdRc. (110.11)

Если же известны координаты спутника С, а координаты точки М определяются, то

de==-~QdR. (110.12)

Уравнения (110.11) и (110.12) представляют собой системы трех уравнений с тремя неизвестными параметрами и могут быть однозначно разрешены. Значит, для определения координат спутника С, при известных координатах точки М, достаточно определить с одной станции а, б, г. То же справедливо и для решения обратной задачи. Поэтому будем рассматривать лишь задачу определения координат спутника С, т. е. только уравнение (110.11), так как все выводы для обратной задачи получаются аналогично. Будем считать, что наблюдения производились синхронно.

Предположим, что на станции М измерено только топоцентрическое расстояние г до спутника. Тогда возникает лишь одно (последнее) уравнение системы (110.11), а именно:

dr = (cos а cos б sin а cos б sin б) dRc.

(110.13)

Здесь а и 6 вычисляются по приближенным формулам координатам точек М и С. Совершенно очевидно, что для определения вектора dRc необходимо иметь три уравнения типа (110.13), что может быть получено лишь при синхронных* наблюдениях топоцентрических расстояний г с трех станций. Тогда вместо уравнений (110.11) получим систему уравнений вида

/cosaiCOs6i sinai cos6i sin6i\ созазСозбз sin 2 COS бз sin62 Vcosaocos6o sinaocos6q sin б,/

(110.14)

Если на наземной станции измерялись лишь топоцентрические угловые координаты а и б, то возникают лишь два первых уравнения системы (110.11):

-cos а sin б

cos б da)

-since

-sinа-cosб cos6\

cos a

. (110.15)

Этих уравнений также недостаточно для определения всех трех параметров dXc-, dYc, dZc. Поэтому нужно производить наблюдения по крайней мере с двух наземных станций. Тогда получаем систему уравнений

db[ cos б dai

db cos 62 dal

--г-cosai cos6i--7--sinai-sin6i

- - cos Oj

sm ai

cos a.

1/1 1

--7-COSaa sin62--r- sina2 sin62 -7--cos 62

) I

--smaa

cos aa

dX dY dZ

(110.16)

Система (110.16) содержит избыточные измерения и поэтому должна решаться по способу наименьших квадратов.

2. Метод синхронных наблюдений

Предположим, что имеется сеть космической триангуляции, содержащая п -\- т наземных станций, причем координаты п станций {i = i, i, . . ., ii) известны, a координаты m станций (/ = = /х /2 7m) определяются. Пусть для построения сети космической триангуляции производились синхронные наблюдения S положений ИСЗ {к = к, к, . . kg). Наблюдения некоторых положений ИСЗ производились как с определяемых, так и с известных станций, но каждое положение ИСЗ наблюдалось обязательно с нескольких станций (не менее двух). С каждой станции наблюдались либо все, либо некоторые из элементов а, б, г. Обозначим матрицу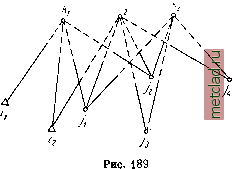