где / - некоторый постоянный вектор, называемый вектором Лапласа.

Уравнение (108.28) называют уравнением Лапласа. Нетрудно убедиться, что вектор с ортогонален вектору /, т. е.

1/1+2/2 + 3/3 = 0. (108.29)

Вектор с ортогонален плоскости орбиты, а вектор / лежит в этой плоскости и определяет фокальную ось орбиты. Умножив (108.28) скалярно на г и сложив все три получившихся уравнения, получим

/1+ /2У + /з2 = -}хг+ с\ (108.30)

Уравнения (108.23) и (108.30) полностью определяют орбиту. Как следует из них, орбита есть линия пересечения поверхности вравдения второго порядка, задаваемой уравнением (108.30), и плоскости (108.23), в которой лежит фокальная ось этой поверхности.

Так как движение происходит в плоскости (108.23), то удобно перейти к новой системе координат , т), , направив ось по вектору кинетического момента с, а оси ит] расположив в плоскости орбиты, причем ось направить по вектору Лапласа /. Тогда переход от координат в системе х, у, zk координатам в системе ,ri, t определится следую1цим образом:

(108.31)

В новых координатах уравнение (108.23) запишется как

= 0,

а уравнение (108.30) примет вид

pir4-/l = c2.

Введя в плоскости от] полярную систему координат г, получим

= r-C0S6 ]

цг-sinтЭ j *

В полярной системе координат уравнение (108.33) примет вид

яг -- /г - cos О = с.

(108.32) (108.33)

(108.34)

откуда

l-f--cosO

Введем обозначения

С2 /

(108.35) (108.36)

(108.37)

и тогда уравнение (108.36) запишется в виде

(108.38)

1-\-е- cos й

которое и является полярным уравнением орбиты.

Орбита является круговой при е = О, эллиптической при О <Се << 1, параболической при е = 1, гиперболической при е >>1.

В новой системе координат , т], формулы (108.21) примут вид

U-lt = o\, (108.39)

Iri - nt

так как = О и = 0. Третье уравнение с учетом (108.34) примет вид

г = с (108.40)

и дает возможность найти зависимость угла & от времени.

Плоскость орбиты спутника, движущегося в центральном поле, проходит через начало координат и пересекает плоскость экватора вдоль линии узлов 0Q (рис. 184). Точка, в которой спутник пересекает плоскость экватора с юга на север, называется восходящим узлом. Угол XOQ называется долготой восходящего узла и обозначается Q. Угол между касательной в восходящем узле к орбите в направлении движения тела и касательной к экватору в направлении оси F называется наклонением орбиты и обозначается через i. Угол i изменяется от 0° до 180°, причем если i превышает 90°, то считают, что движение обратное. Углы Q и i определяют ориентацию плоскости орбиты в пространстве. Угол QOn, отсчитываемый в направлении движения по орбите, определяет положение перигея п и обозначается через со. Он называется расстоянием перигея от узла и определяет ориентацию орбиты

в ее плоскости. Угол пОС называется истинной аномалией и обозначается через Элементы а - большая полуось же - эксцентриситет определяют форму и размеры орбиты. Время вводится посредством задания т - момента прохождения перигея. Таким образом, а, е, i, Q, о) -- и т могут рассматриваться как шесть независимых элементов, которые полностью определяют орбиту и положение тела на орбите в любой момент времени.

Установим связь постоянных интегрирования с и / и элементов орбиты. На основании (108.38) и (108.39) запишем

ТТ--йГ-4 = с (108.41)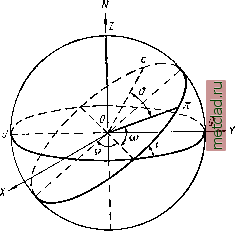

Рис. 184

* = -f-lT+7W- (108.42)

Возьмем интеграл от момента прохождения ИСЗ через перицентр т до момента t, соответственно -д- изменится от нуля до д. Имеем

t- = -{-rn--. (108.43)

с J (1-f е-COS 0) о

Будем полагать, что движение эллиптическое, т. е. О <Се <<1. Введем новую угловую переменную е (эксцентрическая аномалия), определяемую следующей подстановкой

Ч=У-Ч\- (108.44)

Отсюда имеем

sec2 -dE= Y~T Т (108.45)

следовательно,

- Eosi (108.6)

Далее имеем

l + e.cosd = l + e-= , ~ , . (108.47)

Подставляя полученные выражения в интеграл (108.43), найдем

(* Г (1 -ecos£)d£: 1 . . /ло /о\

J (i+.cos#r- =j =7T3;;)vr(g- °g) (108.8)

- = и - (108.49)

с (1-2) /2

Так как для эллипса справедливо соотношение

i - e

и учитывая

(108.50)

найдем окончательно

Xf ( -т) = Е -е sin (108.51)

Это уравнение называется уравнением Кеплера и дает искомую зависимость угла е от времени. Величина

пХ (108.52)