вием будет линейность изменения Из этого условия одновременно следует, что-смежные точки нивелирования должны быть достаточно близки.

Опытные данные позволили установить, что поставленное условие во многих случаях будет выполняться с некоторой приемлемой точностью, если расстояние S между смежными точками нивелирования будет порядка 10-20 км в равнинной местности с плавными и равномерными изменениями уклонений отвесных линий и 3-5 км в горных и аномальных районах.

Однако и при таких расстояниях могут быть заметные отступления от пред- положенного закона линейного изменения уклонения снижающие точность, нивелирования.

Рабочие формулы для вычисления превышений точек квазигеоида при некотором конечном значении s в рассматриваемом случае получатся следу-юпщм образом.

Возьмем некоторую линию астрономического или астрономо-гравиметри- ческого нивелирования от прежней начальной точки А до некоторой точки Б. Пусть ММi - две произвольные смежные точки этой линии нивелирования, (рис. 140).

Введем обозначения:

Ol и в2 - уклонения отвесных линий в точках М и М-; Sm - расстояние ММ,

Учитывая предположенную линейность измерения Ь, можем написать:

ksM hi

(73.3).

Тогда на основании формулы (73.1) получим для интервала ММ-

ds= ~

(73.4)

Рассматривая линию АВ, состоящую из отрезков, аналогичных ММ-,. получаем для нее

=~- i = (1 + 2+3+. .) =

(73.5).

Остановимся на специфических особенностях и различии обоих методов, нивелирования.

В методе астрономического нивелирования уклонения О получаются из астрономических и геодезических измерений, т. е. по формуле

= Lr cos--riaj,sin, (73.6)

11г = Ц - В- о, 171 Я sin 25, nip = {К -L) cos S,

А - азимут вертикальной плоскости, в которой расположен данный отрезок линии нивелирования.

Отсюда следует, что в каждой точке хода астрономического нивелирования должны быть известны астрономические и геодезические координаты. Иначе говоря, если ход астрономического нивелирования расположен по ряду триангуляции 1 класса, то на каждом пункте, а в большинстве районов и между ними, на пунктах 2 и даже 3 класса должны выполняться точные астрономические определения широт и долгот.

При астрономо-гравиметрическом нивелировании уклонения отвесных линий Ь при вычислении интеграла J bds определяются по методу, изложенному в § 66. Для этого необходимо иметь сравнительно редкую сеть совмеп1;енных астрономических и геодезических пунктов, для которых величины аг>т]аг вдг ВЫЧИСЛЯЮТ ПО формулам (65.17) и (65.19). Тогда уклонения отвесных линий в точках, расположенных между астрономо-геодезическими пунктами, получаются путем интерполирования с привлечением результатов гравиметрической съемки. В этом случае уклонения отвеса между астрономо-геодезическими пунктами могут быть вычислены как угодно часто. Точнее говоря, уклонения отвесных линий в этом случае могут быть весьма точно проинтерполированы между редкими астрономо-геодезическими пунктами. Поэтому для астрономо-гравиметрического нивелирования интеграл J bds может быть вычислен точно, без какого-либо предположения о характере изменений б*.

Из сказанного ясно вытекает преимуп1;ество астрономо-гравиметрического метода нивелирования по сравнению с астрономическим методом. Метод астрономо-гравиметрического нивелирования позволяет без существенных дополнительных затрат труда получать высоты квазигеоида с достаточной строгостью и точностью. Ошибки определения высот по этому методу могут быть (при соответствующей, реально выполнимой программе полевых измерений) доведены до весьма малых величин.

Идея астрономо-гравиметрического нивелирования была предложена Ф. Н. Красовским и разработана М. С. Молоденским, под руководством которого выполнены обширные теоретические исследования по обоснованию и анализу различных сторон этого метода.

1. Формулы астрономического нивелирования

Приведем вывод формулы астрономического нивелирования, впервые полученной М. С. Молоденским.

Пусть дана на поверхности Земли точка М, имеющая геодезическую высоту Н = Саг Над референц-эллипсоидом (рис 141). Возьмем точку Mi, расположенную от точки М на бесконечно малом расстоянии ds, имеющем азимут А.

Далее пусть:

2геод и астр - гоодезический И астрономичоский зенит точки М; ©аг - составляющая угла между 2геод и ZacTp в рассматриваемой плоскости;

dH = Мк ж dh == MiL - элементарные превышения точки Afj над точкой М относительно референц-эллипсоида (Я = const) и уровенной поверхности точки М {W = const) соответственно;

ds = Мк - проекция отрезка ds на поверхность Н = const (или и = = const - по малости угла е).

Получим проекцию ломаной МкМ на отвесную линию, равную отрезку MiL = dh. Действительно, из рис. 141 получаем

= с? (Я + Саг) cos ваг + d ?H sin ваг

или, пренебрегая величинами порядка в,

dh = d (Я + Саг) +ваг dsH = dH вр ds.

dB = dh - ваг dsji.

Откуда

(73.7)

(73.8) (73.9)

Из формулы (73.8) следует, что превышения точек земной поверхности относительно референц-эллипсоида могут определяться на основе астрономических и геодезических измерений, без привлечения гравиметрических данных, т. е. чисто геометрически. Действительно, dh - превышение, полу-d.Hd(Hf*i,ug) чаемое непосредственно из геометрического нивелирования, ds -

.-у-const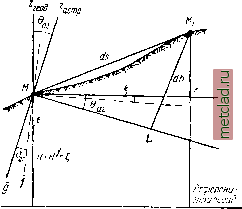

- --const

wConst

Рис. 141

Рис. 142

элемент линейного расстояния, получаемого из триангуляции, а 0 - угол, вычисляемый как функция астрономических и геодезических координат по формуле (65.19).

Если имеем ряд последовательных передач высоты от точки М через превышения dh между точками ММ, М-М, ММ, . . ., Mk-i, Mk (рис. 142), то разность высот Нм - Я, считаемая по нормали от референц-эллипсоида, определится так:

Ям,-я

\ dh-{ м м

Sds.

(73.10)

Полученная формула практического значения не имеет; для ее использования необходимо было бы на каждой станции нивелирования иметь астрономические и геодезические координаты.

Для решения задач высшей геодезии необходимо знать высоту Я для каждого пункта триангуляции (полигонометрии) высших классов; для которых нормальные высоты заранее определены из геометрического нивелирования. Следовательно, для вычисления Я по формуле Я = Я -j- С необходимо получить формулу для вычисления приращений аномалий высот dt или, иначе, приращений высот квазигеоида над референц -эллипсоидом.

Но если из чисто геометрических измерений оказалось возможным строго выразить сумму слагаемых Н + t, = Н* то каждое из этих слагаемых может