1000 до 800 м/ск----800 550.И/СК

550 И9 м/ск

419 375Л1/ск

375 295 м/ск

295 240 м/ск

240 малых.....

оружия И продолговатых снарядов послужило сильным толчком для изучения законов сопротивления воздуха полету снаряда. В результате опытов Башфорта в Англии (1865 - 1880 гг.) над продолговатыми и над сферическими снарядами, на основании работ Маиевского в России (1868- 1869 гг.), завода Крупна в Германии (1881- 1890 гг.) и Хожеля в Голландии (1884 г.) оказалось возможным выразить силу сопротивления воздуха Q таким одночленом:

= XAnR ~ , где Я - коэфф., зависящий

от формы снаряда, А-численный коэфф., я-отношение длины окружности к диам., R - радиус цилиндрической части снаряда, П--плотность воздуха при стрельбе и iIo= = 1,206 кг - плотность воздуха при 15°, давлении атмосферы в 750 мм и влажности 50%. Коэффициент А и показатель п опре-ляются из опыта и различны для разных скоростей, а именно:

Для скор, от 1000 до 800 Л1/ск А=0,7130; п-1,55

.4=0,2616; П-=1,70 А =0,0394; П=2 А=0,0*940; Т?=3 Л=0,0670; л=5 А =0,0*533; П=3 А=0,0140; п=2

Общие свойства траектории невращающе-гося снаряда в воздухе устанавливаются на основании дифференциальных ур-ий движения его ц. т. в вертикальной плоскости стрельбы. Эти уравнения имеют вид:

dx =----v\ - ; dt = ----

д cosO д cos 6

в них: Q - сила сопротивления воздуха, Р-вес снаряда, 9 - угол наклона касательной в данной точке траектории к горизонту, V - скорость снаряда в данной точке, Vi=vcos б-гориз. проекция скорости, S - длина дуги траектории, t - время, д- ускорение силы тялсести. На основании этих ур-ий С.-Робер указал такие главные свойства траектории: она выгнута выше горизонта, вершина ее находится ближе к точке падения, угол падения больше угла бросания, гориз. проекция скорости постепенно убывает, наименьшая скорость и наибольшая кривизна траектории находятся за вершиной, нисходящая ветвь траектории имеет ассимптоту. Проф. Н. Забудским, кроме того, добав.яеио, что время полета в нисходящей ветви больше, чем в восходящей. Траектория снаряда в воздухе изображена на фиг. 2. При движении снаряда в воздухе уго.д наибольшей дальности вообще меньше 45°, но м. б. случаи, когда этот угол больше 45°. Дифференциальные ур-ия движения ц. т. снаряда не интегрируются, и поэтому основная задача внешней Б. в общем случае не имеет точного решения. Довольно удобный способ приближенного решения был дан впервые Дидионом. В 1880 г. Сиаччи предложил удобный для практики способ решения задачи прицельной стрельбы (т.е. когда 15°), приме-

cose rf9

няемый и доныне. Для удобства вычислений Сиаччи составлены соответствующие таблицы. Для решения задач навесной стрельбы (т. е. при >15°), когда начальная скорость меньше 240 м/ск, дан способ и Составлены необходимые таблицы Отто, измененные впоследствии Сиаччи и Лордильоном. Баш-форт также дает способ и таблицы для решения задач навесной стрельбы при скоростях свыше 240 м/ск. Проф. Н. Забудский для решения задач навесной стрельбы при начальных скоростях от 240 до 650 м/ск принимает силу сопротивления воздуха пропорциональной 4-й степени скорости и дает способ решения при этом допущении. При начальных скоростях, превосходящих 650 м/ск, для решения задач навесной стрельбы приходится разбивать траекторию на три части, при чем крайние части вычислять по способу Сиаччи, а среднюю-но способу Забудского. За последние годы получил широкое распространение и общее признание способ решения основной задачи внешней В., основанный на методе Штер-мера - численного интегрирования дифференциальных ур-ий. Применение этого метода к решению задач Б. было впервые произведено акад. А. Н. Крыловым. Метод численного интегрирования является универсальным, т. к. пригоден для любых скоростей и углов бросания. При этом способе легко и с большой точностью м. б- учтено изменение плотности воздуха с высотой Это последнее имеет большое значение при стрельбе под большими углами бросания, до 90°, со значительными начальными скоростями, порядка 800-1 ООО м/ск (стрельба по воздушным целям), и особенно при так называемой сверхдальней стрельбе, т. е. па дистанцию 100 и более км.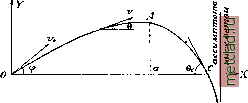

Фиг. 2. Траектория снаряда в воздухе: OA-восходящая ветвь траектории, АС - нисходящая ветвь траектории. А-вершина траектории.

Основанием для решения вопроса о стрельбе на такие дистанции служит следующая идея. Снаряд, выпущенный с очень большой начальной скоростью, например 1500 м/ск, под углом бросания 50--55°, быстро долетает в восходящей ветви своей траектории до таких слоев атмосферы, в которых плотность воздуха чрезвычайно мала. Считают, что на высоте 20 км плотность воздуха в 15 раз, а на высоте 40 км в 350 раз меньше плотности воздуха на поверхности земли; вследствие этого в такое же соответственно количество раз на этих высотах уменьшается и сила сопротивления воздуха. Т.о. можно считать часть траектории, проходящую в слоях атмосферы, ле1ка-щих выше 20 км, параболой. Если же касательная к траектории па высоте 20 км будет иметь наклон к горизонту в 45°, то

дальность но безвоздушному пространству будет наибольшей. Чтобы обеспечить угол в 45° на высоте 20 км, нужно снаряд бросить с земли под углом, большим 45°, т. е. под углом в 50-55°, в зависимости от начальной скорости, калибра и веса снаряда. Например (фиг. 3): снаряд, брошен, под углом к горизонту в 55° с начальной скоростью в 1 500 м/ск; в точке а восходяш;ей ветви его скорость стала равна 1 ООО м/ск, а касательная к траектории в этой точке

Фиг. 3. Траектория полета снаряда.

составляет с горизонтом угол в 45°. При этих условиях дальность полета аЪ по безвоздушному пространству будет составлять:

1 0002 sin 90° X =--= 102 KM, а дальность по

горизонту точки стояния орудия ОС будет более 102 км на сумму участков OA и ВС, вычисление величины к-рых удобнее и точнее всего можно произвести способом численного интегрирования. При точном расчете сверхдальней траектории приходится принимать во внимание влияние враш;ения земли, а для траекторий с дальностью в несколько сот км (теоретически возможный случай) также шарообразную форму земли и изменение ускорения силы тяжести как по величине, так и по направлению.

Первые суш;ественные теоретическ, исследования движения продолговатого снаряда, вращающегося около своей оси, были произведены в 1859 г. С.-Робером, мемуары которого послужили .основой для работ по этому вопросу Маиевского в России. Аналитические исследования привели Маиевского к заключению, что ось фигуры снаряда, когда поступательная скорость не слишком мала, имеет колебательное двилсение вокруг касательной к траектории, и позволили изучить это двилсение для случая прицельной стрельбы. Де-Спарре удалось привести эту задачу к квадратурам, а проф. Н. Забуд-скому-распространить вывод де-Снарре на случай навесной стрельбы. Дифференциальные уравнения вращательного движения снаряда при принятии некоторых практически возможных допущений имеют вид: М = - cos V db;

, ic J. , sinv , d-i = -dt -H db;

здесь: J-угол меледу касательной к траектории и осью фигуры снаряда; v - угол меледу вертикальной плоскостью, проходящей через ось канала орудия, и плоскостью, проходящей через касательную к траектории и ось фигуры снаряда; к - момент силы сопротивления воздуха относительно ц. т. снаряда; А - момент инерции

т. о. т. п.

снаряда относительно оси; Рц -проекция угл. скорости вращения снаряда на его ось; 0 - угол наклона касательной в данной точке траектории к горизонту; t - время.

Эти уравнения точно не интегрируются. Исследование вращательного движения продолговатого снаряда приводит к следующему основному выводу: при прицельной стрельбе ось снаряда всегда отклонена в одну сторону от плоскости стрельбы, а именно - в сторону вращения снаряда, если смотреть на него сзади; при навесной стрельбе это отклонение может быть и в обратную сторону. Если представить себе плоскость, всегда остающуюся перпендикулярной к касательной к траектории и отстоящую во время полета снаряда всегда на одном и том же расстоянии от его ц. т., то ось фигуры снаряда вычертит на этой плоскости слолсную кривую вида, показанного на фиг. 4. Большие петли этой кривой являются результатом колебательного движения оси фигуры снаряда вокруг ка- -. сательной к тра- Л ектории, это - fiC т. н. прецессия; малые же петли и . , кпттиэтптпртк wnw- - Кривая движения

ВОЛНИСТОСТЬ кри- ОСИ снаряда.

ВОЙ есть результат несовпадения мгновенной оси вращения снаряда с осью его фигуры, это - так наз. нутация. Для получения большей меткости снаряда необходимо добиваться уменьшения нутации. Отклонение снаряда от плоскости стрельбы вследствие отклонения его оси называется деривацией. Маиев-ским выведена простая формула для величины деривации при прицельной стрельбе; эта же ф-ла м. б. применена и при навесной стрельбе. Вследствие деривации проекция траектории на горизонт, плоскость получает вид, указанный на фиг. 5. Т. о. траектория вращающегося снаряда является кривой двоякой кривизны. Для правильного полета продолговатого снаряда ему необходимо придать соответствующую скорость

проекция плоскости стрельбы

оруЪие

Фиг. 5. Горизонтальная проекция плоскости стрельбы и траектории снаряда: аЬ-деривация.

вращения вокруг оси. Проф. Н. Забудский дает выралсение минимальной скорости вращения, необходимой для устойчивости снаряда на полете в зависимости от его конструктивных данных. Вопросы вращательного движения снаряда и влияния этого двилсе-ния на полет его крайне сложны и мало изучены. Лишь за последние годы предпринят ряд серьезных исследований этого вопроса гл. обр. во Франции, а таклее и в Америке.

Изучение действия снарядов но различным предметам ведется внешней Б. гл. обр. путем опытов. На основании опытов Мец-кой комиссии даны формулы для вычисле-1ШЯ величин углублений снарядов в твердые среды. Опыты Гаврской комиссии дали материал для вывода ф-л пробивания брони.

Испанский артиллерист де-ла-Лав на основании опыта дал формулы для вычисления объема воронки, образующейся при разрыве снаряда в грунте; объем этот пропорционален весу разрывного заряда и зависит от скорости падения снаряда, его формы, качества грунта и свойств взрывчатого вещества. Способы рещения задач внещней Б. служат основанием для составления таблиц стрельбы. Вычисление табличных данных производится после определения стрельбой на 2-3 дистанции нек-рых коэффициентов, характеризующих снаряд и орудие.

Внутренняя Б. рассматривает законы движения снаряда в канале орудия под действием пороховых газов. Только зная эти законы, молено проектировать орудие требуемой мощности. Т. о. основная задача внутренней Б. заключается в установлении функциональной зависимости давления пороховых газов и скорости движения снаряда в канале от проходимого им пути. Для уста-новлеьшя этой зависимости внутренняя Б. пользуется законами термодинамики, термохимии и кинетической теории газов. С.-Робер первый воспользовался началами термодинамики при изучении вопросов внутренней В.; затем французский инж. Сарро дал ряд капитальных трудов (1873-1883 гг.) по вопросам внутренней В., послуживших основой для дальнейших работ различных ученых, и этим положил начало современному рациональному изучению вопроса. Явления, происходящие в канале данного орудия, существенным образом зависят от состава пороха, формы и размеров его зерен. Продолжительность горения порохов. зерна зависит главн. образ, от его наименьшего размера-толщины-и скорости горения пороха, т. е. быстроты проникания пламени в толщу зерна. Скорость горения прежде всего зависит от давления, под которым оно происходит, а таклсе и от природы пороха. Невозможность точного изучения горения пороха заставляет прибегать к опытам, гипотезам и допущениям, упрощающим решение общей задачи. Сарро выразил скорость горения и пороха такой функцией давления Р: и=АР, где А - скорость горения при давлении в 1 кг/см, а v - показатель, зависящий от сорта пороха; v, вообще говоря, меньше единицы, но очень близка к ней, поэтому Себер и Гюгоньо упростили формулу Сарро, приняв v=l. При горении под переменным давлением, что имеет место в канале орудия, скорость горения пороха является также величиной переменной. Согласно работ Вьеля молшо считать, что бездымные пороха горят концентрическими слоями, горение же дымных порохов такому закону не подчиняется и происходит весьма неправильно. Закон развития давлений пороховых газов в закрытых сосудах установлен Ноблем в таком виде: ВТхШ RTxd fd

Р=--

W-a(o

где R =

1-ttd

давление атмосферы;

роха; TF-объем сосуда, в к-ром происходит сгорание; w-вес заряда; -коволюм, т. е. объем продуктов разлолсения 1 кг пороха при бесконечно большом давлении (вообще принимают а=0,001м;о); d-плотность заряжания, равная при метрических мерах

/=JZTi-сила пороха, измеряемая в единицах работы на единицу веса заряда. Для упрощения решения общей задачи о движении снаряда в канале орудия предполагают: 1) что воспламенение всего заряда происходит одновременно, 2) что скорость горения пороха в течение всего процесса пропорциональна давлению, 3) что горение зерен происходит концентрическими слоями, 4) что количество теплоты, отделяемое каждой равной долей заряда, объемы и состав газов, а также сила пороха постоянны во все время горения заряда, 5) что нет передачи теплоты стенкам орудия и снаряду, 6) что нет никаких потерь газов и 7) что нет волнообразного двюкения продуктов взрыва. Принимая эти основные допущения и еш,е некоторые, различные авторы дают решение основной задачи внутренней Б. в виде той или иной системы дифференциальных ур-ий движения снаряда. Интегрировать в общем виде эти ур-ия не представляется возможным, а потому прибегают к прибли-лсенным методам решения. В,основе всех этих методов лежит классическое решение задачи внутренней Б., предложенное Сарро и заключающееся в интегрировании дифференциальных ур-ий движения снаряда помощью залгены переменных. После классических формул Сарро наиболее известными являются формулы, предложенные Шарбо-нье и Сюго. Баллистики Бианки (Италия),

го-объем продуктов разложения 1 кг пороха при 0° и давлении 760 мм, считая воду газообразной; Ti-абс. темп-ра разложения по-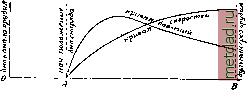

фиг. 6. Диаграмма скоростей снаряда и давлений газов в канале орудия: А В-полный путь снаряда по каналу, OA-длина зарядной каморы.

Кранц(Германия) и Дроздов(Россия)таклсе дают свои методы решения основной задачи. Все вышеуказанные методы представляют значительные трудности для практического применения вследствие их сложности и необходимости таблиц для вычисления различного рода вспомогательных функций. Методом численного интегрирования дифференциальных уравнений задача внутренней Б. таклсе м. б. решена. Для практических целей некоторыми авторами даются эмпирические зависимости, пользуясь к-рыми можно достаточно точно решать задачи внутренней Б. Наиболее удовлетворительными из таких зависимостей являются ф-лы Гейденрейха, ле-Дюка, Оккинггауза (Oekkingliaus) и дифференциальные формулы Киснемского. Закон развития давления и закон скоростей движения снаряда в канале орудия графически представлены на фиг. 6.